Introduction
Asteroids formed five billion years ago in the solar system. Having failed to integrate with planets, they are the largest space rocks orbiting the Sun. Their size ranges from a few meters to hundreds of kilometres across, and their weight is much less than the moon. As a result of their formation and impacts, they have irregular shapes. Their heterogeneous surfaces are also heavily cratered. What is the shortest path between two distinct points on the surface of the asteroid?
To find such a path, I start by uploading the asteroids' data$^1$. Examples of asteroids are as follows.  The centre of these 3-dimensional objects is not usually at the origin of the Cartesian coordinate system. For example, the centre of the asteroid Lutetia is
The centre of these 3-dimensional objects is not usually at the origin of the Cartesian coordinate system. For example, the centre of the asteroid Lutetia is
In[1]:= {centreLutetia, centreAtlas,
centreKleopatra} = {RegionCentroid[Lutetia], RegionCentroid[Atlas],
RegionCentroid[Kleopatra]}
Out[1]= {{1.61516, 2.69139,
0.94739}, {-0.0687444, -0.0167443, -0.0472993}, {0.545271, \
-0.0145182, -0.531176}}
It is convenient to express the Cartesian coordinates of the asteroid's surface in Spherical coordinate. This function updates the coordinates so that the centre of the asteroid is at the origin of the Cartesian coordinate system. Then, it transforms the Cartesian coordinates into spherical coordinates.
findSphericalCoordinates[data_, centre_] :=
Module[{vertices, r, ?, ?},
vertices =
Map[# - centre &, Cases[data, {"v", x_, y_, z_} -> {x, y, z}]];
{r, ?, ?} =
Transpose[ToSphericalCoordinates[vertices]];
Transpose[{?, ?, r}]
]
These spherical coordinates $\left\{r_i,\theta _i,\phi _i\right\}_{i\in A}$, where $A$ is the set containing all the spherical coordinates, are a discrete representation of the surface of the asteroid Lutetia.
To find the shortest path, I first calculate a smooth 2-dimensional curve for the surface of the asteroid. Then, I apply differential geometry to calculate the geodesic. This approach requires solving two second order partial differential equations.
The surface of the asteroid
Spherical harmonic approximation
In the spherical coordinate system, we have $0\leq \theta \leq \pi$ and $-\pi <\phi \leq \pi$ . Because the surface of the asteroid is irregular, the radius is a function of the polar angle and the azimuthal angle $r=r(\theta ,\phi )$. To calculate the radius $r(\theta ,\phi )$ of the asteroid, I use a linear superposition of spherical harmonics $Y_l^m (\theta,\phi)$, where $l\geq 0$ is an integer and $-l\leq m\leq l$. This linear superposition will approximate the radius of the asteroid.
As a result, $r(\theta,\phi)\simeq\sum_{l=0}^{l_{Max}}\sum_{m=-l}^{l} a_{lm} Y_l^m (\theta,\phi)$, where $l_{Max}$ is a positive number defining the order of the approximation, and $a_{l m}$ is a constant coefficient of the linear superposition$^2$. For any positive integer $l_{Max}$, the spherical harmonics are
With[{lMax = 8}, formFit = findFormFit[lMax]];
This list contains $(l_{Max}+1)^2$ spherical harmonics. The coefficients Subscript[a, l m] are found using the linear fit model.
Plot of Lutetia's surface
For the asteroid Lutetia, the coefficients $a_{l m}$ are
rLinLutetia = LinearModelFit[coordSphLutetia, formFit, {?, ?}]

Percentage error
To calculate the error introduced by the linear expansion of the spherical harmonics, I calculate for each point $(\theta,\phi)$ the percentage error between the fitted radius and the radius imported from the NASA's data. 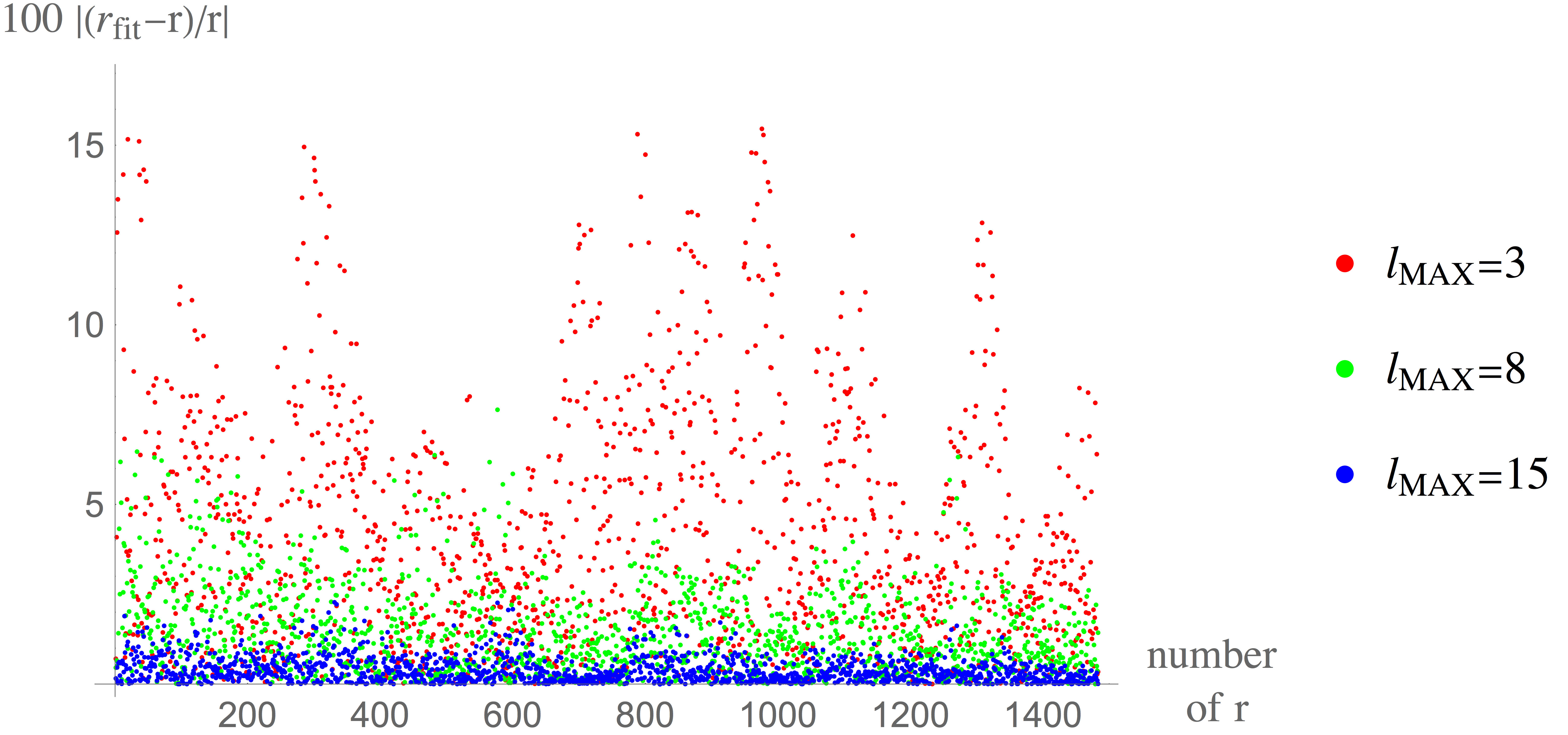
The geodesic
Metric Tensor
To calculate the geodesic, I will solve the differential equation of the geodesic$^3$. The geodesic is a line on the surface of the asteroid. This surface is a 2-dimensional curved space embedded in a 3-dimensional space. As a result, the base vectors of the surface change for different locations on the surface. The metric is the second rank tensor $g_{\alpha\beta}$ which depends on base vectors. The Greek indices $\alpha,\beta\in\{\theta,\phi\}$. The operational form of the metric tensor is
Og[?_, ?_] = {{#^2 + D[#, ?]^2, D[#, ?] D[#, ?]},
{D[#, ?] D[#, ?], #^2 Sin[?]^2 + D[#, ?]^2}} &
This operator acts on any radial function $r(\theta,\phi)$. The inverse of the matric tensor is $g^{\alpha\beta}$. Its functional form is
OgInv[?_, ?_] =
1/(#^2 Sin[?]^2 + Sin[?]^2 D[#, ?]^2 + D[#, ?]^2) {{Sin[?]^2 + D[#, ?]^2/(#^2) , -
D[#, ?] D[#, ?])/(#^2)}, {-D[#, ?] D[#, ?])/(#^2) ), 1 + D[#, ?]^2/(#^2) }} &
These operators are then used to calculate the metric for a given spherical harmonic approximation. It is convenient to calculate the partial derivatives of the metric tensor $\partial_{\mu} g_{\alpha\beta}$, which is usually written using the compact notation $g_{\alpha\beta,\mu}$.
Christoffel symbol
The Christoffer symbols $\Gamma_{\beta\mu}^{\gamma}$ provide the change of the base vectors over the smooth surface. They are calculated using the Arfken (1985, p. 161) definition and the metric tensor in the previous section.
Geo function
Let $\lambda$ be the parameter on the geodesic. The parametric expression of the geodesic then becomes $(x^\theta(\lambda),x^\phi(\lambda))$. The two non-linear second order differential equations for the geodesic are $\ddot{x}^\mu+\Gamma_{\alpha\beta}^{\mu}\dot{x}^\alpha\dot{x}^\beta=0$. These two equations are
eq1 = ?''[?] + ?Fit?[?[?],?[?]][[1, 1]] ?'[?]^2
+2 ?Fit?[?[?], ?[?]][[1, 2]] ?'[?] ?'[?] +?Fit?[?[?], ?[?]][[1,1]] ?'[?]^2;
eq2 = ?''[?] + ?Fit?[?[?],?[?]][[1, 1]] ?'[?]^2 +
2 ?Fit?[?[?], ?[?]][[1,2]] ?'[?] ?'[?] + ?Fit?[?[?], ?[?]][[1, 1]] ?'[?]^2;
Let $\lambda\in[\lambda_a,\lambda_b]$ be the integration domain of the geodesic. For example, let $x^\theta(\lambda_a)=\frac{\pi}{12}, x^\phi(\lambda_a)=0, \frac{dx^\theta}{d\lambda}(\lambda_a)=1$ and $\frac{dx^\phi}{d\lambda}(\lambda_a)=1$ be the boundary conditions of the differential equation. The solution of the differential equations then becomes
?a = 0;
?b = 2.8;
sol = NDSolve[{eq1 == 0, eq2 == 0,
?[0] == ?/12, ?[0] == 0, ?'[0] == 1, ?'[0] == -1}, {?[?], ?[?]}, {?, ?a, ?b}]
The geodesic is
geo?[?_] := Evaluate[?[?] /. sol]
geo?[?_] := Evaluate[?[?] /. sol]
geoFunction[?_] :=
Evaluate[First@rFitLutetia[geo?[?], geo?[?]]
{First@Sin[geo?[?]] First@Cos[geo?[?]],
First@Sin[geo?[?]] First@Sin[geo?[?]],
First@Cos[geo?[?]]}]
It is the red line in these pictures 
Conclusion
The geodesic on the surface of an asteroid is calculated using differential geometry. The asteroid's shape is imported from the NASA databases. Because in this data the asteroid's surface is discrete, a linear superposition of spherical harmonics is used to calculate a smooth 2-dimensional surface. Arbitrary precision can be achieved for larger sets of spherical harmonics. The smooth surface is then used to solve the non-linear second order differential equations for the geodesic. The boundary conditions on the differential equation can be used to define the initial and the final points of the geodesic. For simplicity, in the present notebook, the boundary conditions define the initial point and the rate of change of the geodesic at this point. A limitation of the current geodesic is that the variables $\theta$ and $\phi$ cannot assume values outside their domain. However, for large numbers of geodesic, the functional representation of the Christoffel symbols will reduce the time needed to compute the differential equation. Finally, asteroids are examples of irregular surfaces. Because the geo function does not assume any constraint on the shape of the asteroid's surface, the geo function can be used to calculate the geodesic on any irregular surface.
Acknowledgements
I am grateful to Robert Nachbar, Flip Phillips and Paul Abbott for useful discussion.
References
$^1$ https://sbn.psi.edu/pds/
$^2$ Caitlin R. Nortje, Wil O. C. Ward, Bartosz P. Neuman, and Li Bai. 2015."Spherical Harmonics for Surface Parametrisation and Remeshing," Mathematical Problems in Engineering, vol. 2015, 11 pages. https://doi.org/10.1155/2015/582870.
$^3$Schutz B., 2009. A first course in general relativity. Cambridge university press.