Rafael Guillermo González Acuña
- When the symbolic expressions are very large, they are incomprehensible to most human beings.
- In this work, we present an algorithm that identifies common subexpressions and replaces them with characteristic variables such that is easier to grasp the overall structure of the original expression as well as providing insight into the components of the subexpressions.
First thing that we need to do is replace the Head of the expression in by List. listifyHeads[exprs_List] := Flatten[ReplacePart[#, 0 -> List] & /@ exprs]
listifyHeads[{1 + x^2 - 3 y}]
{1, x^2, -3 y}
Then the next step is to recursively apply this process to all levels of the expression. This is done in the function SubExpression. The function SubExpression gives a list of the expression with common subexpressions replaced, the replacement rules, and subexpression rules. SubExpression::usage =
"SubExpression[expr, depth, count] gives a list of the expression \
with common subexpression replace, the replacement rules, and \
subexpression rules, where depth is the level of complexity of the \
subexpression and count is the number of that subexpression repeats \
in the expression.";
SubExpression[expr_, depth_, count_] :=
Module[{subexprs, replacerules},
subexprs =
DeleteDuplicates[
Select[Flatten[FixedPointList[listifyHeads, {expr}]],
Depth[#] > depth && Count[expr, #, Infinity] >= count &&
Head[#] =!= Power &]];
replacerules = (# ->
Framed[Subscript[\[Alpha],
Flatten[Position[subexprs - (#), 0]][[1]]]]) & /@ subexprs;
{expr //. replacerules, replacerules,
Reverse /@ ((#[[1]] //. DeleteCases[replacerules, #]) -> #[[
2]] & /@ replacerules)}
];
The following expression is an example,
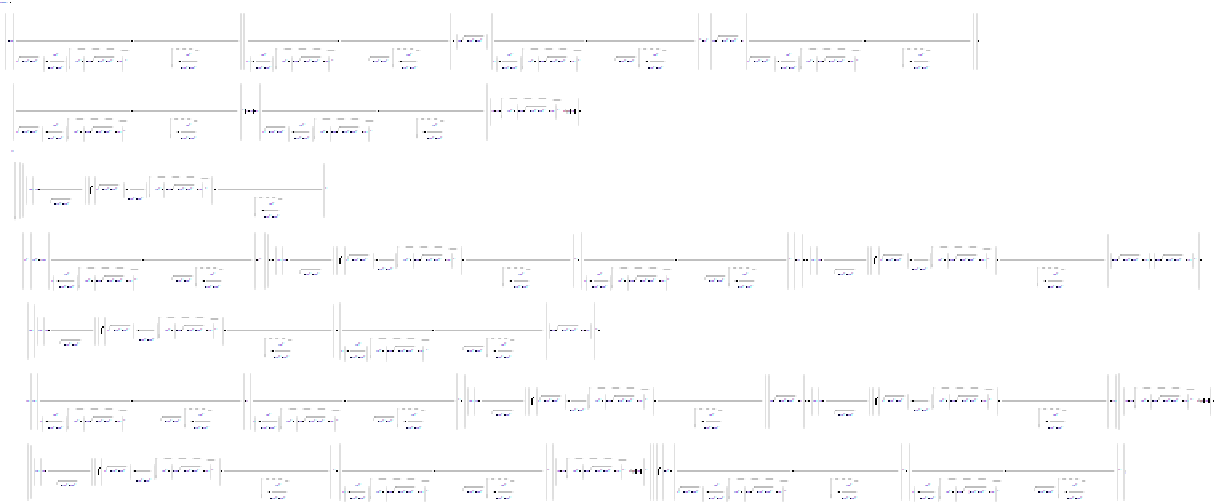
In our first example expr1 we get replacedExpression = the expression in terms of the subexpressions, replacementRules = the replacement rules obtained, subexpressionRule = the value of the subexpressions. {replacedExpression, replacementRules, subexpressionRules} =
SubExpression[expr1, 8, 4]
 - Now we test the replacement is correct, - Now we test the replacement is correct,
test = (expr1 //. replacementRules) //. subexpressionRules;
test == expr1
True
- Now it is interesting to see how the TreeFrom of the expression and their subexpression looks like.
TreeFormToGraph express the TreeFrom in Graph. TreeFormToGraph[treeForm_] :=
Module[{tree = ToExpression@ToBoxes@treeForm, order, pos, label},
label = Cases[tree,
Inset[name_, n_] :> Rule[n, Placed[name, Center]], Infinity];
{order, pos} =
Catenate /@
Cases[tree,
Line[order_] | GraphicsComplex[pos_, ___] :> {order, pos},
Infinity];
Graph[UndirectedEdge @@@ order, VertexLabels -> label,
VertexCoordinates -> MapIndexed[Rule[First[#2], #] &, pos]]]
Here we put the TreeFormToGraph of the subexpressionRules MapAt[TreeFormToGraph,
MapAt[TreeForm, subexpressionRules, {All, 2}], {All, 2}] //
Row[#, Spacer[36]] &
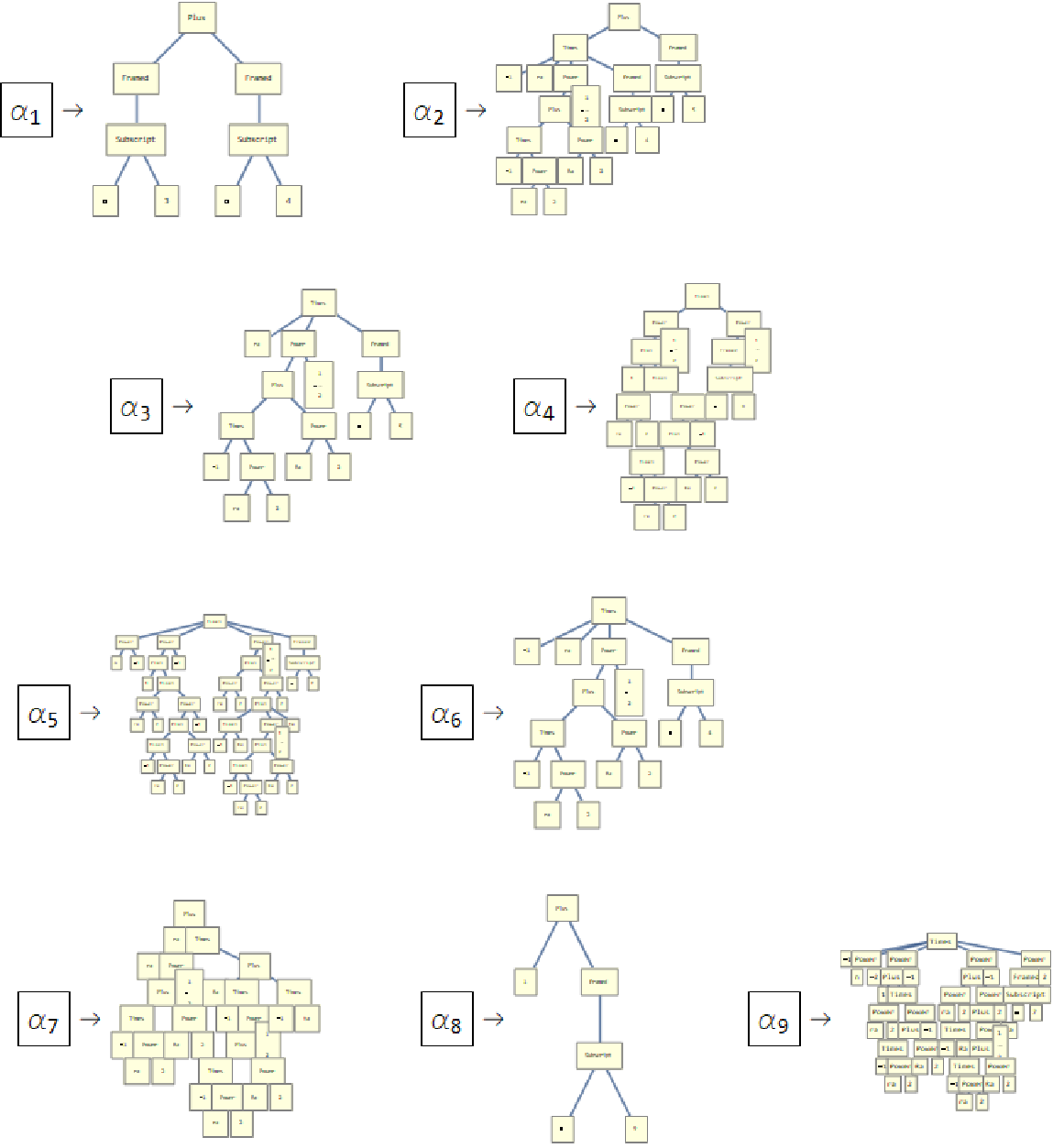
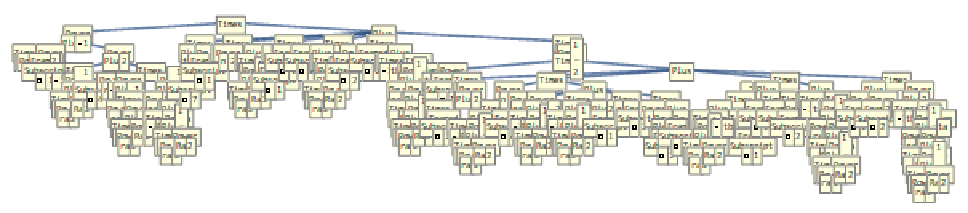 - Finally let's compare our result to the TreeForm of expr1, which is messy - Finally let's compare our result to the TreeForm of expr1, which is messy
TreeFormToGraph[TreeForm[expr1]]

|