A universal Turing machine is a computing machine which can replicate any other Turing machines behavior. Various cellular automaton models have been shown to be Turing universal through their gliders. Gliders are reoccurring structures which interact with other gliders through movement in spacetime.
In this post, A system for automatic detection of universal glider configurations is discussed. In this notebook the Totalistic 2 neighbor cellular automaton rule 624 and 626 are used as examples for this system. The gliders are identified through examining a series of structures and their points with respect to each other. With these gliders, the ending points are found and the systems with common ending points are marked as intersecting. The gliders which are found stemming from these common ending points are interpreted as resulting gliders. These glider intersections are cataloged and then analyzed and combined to determine the ability of the systems to represent the universal Nand Gate.

Figure 1: An array plot of rule 624.
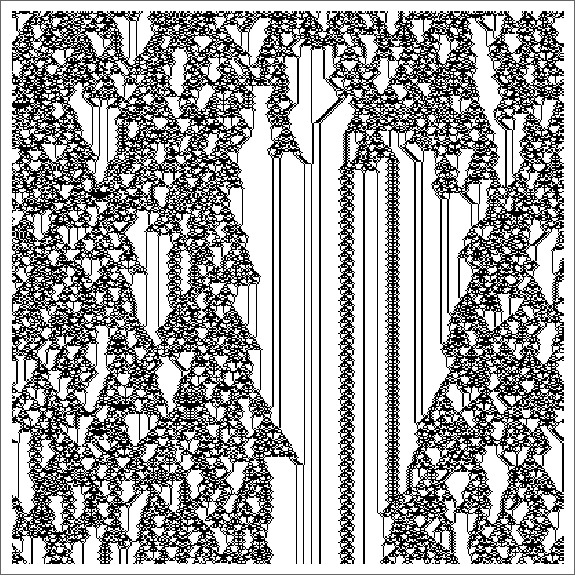
Figure 2: An array plot of rule 626.
Using gliders it is impossible to replicate a Nand gate in the traditional sense as two gliders of the same type can never collide with each other. To avoid this, two separate gliders with different directions can be used per boolean value. In figure 4 (a glider based Nand gate), gliders A and D are be grouped together and gliders C and B are grouped together.
{{0,0}-> 1, {1,0}->1, {0,1}->1, {1,1}->0}
Figure 3: The boolean definition of a Nand gate.
{{b,c}->{a,d},{a,b}->{a,d},{d,b}->{a,d},{a,c}->{a,d},{c,d}->{a,d},{a,d}->{b,c}}
Figure 4: The Glider based definition of a Nand gate.
Below, the graph of a glider interaction is shown. The gliders are shown moving in and out of the interaction. The ones moving toward the intersection point are the initial gliders involved in the collision, the gliders moving away from the intersection point are the gliders produced by the interaction. Systems with both are gliders which both are used as reactants and products in the glider system.
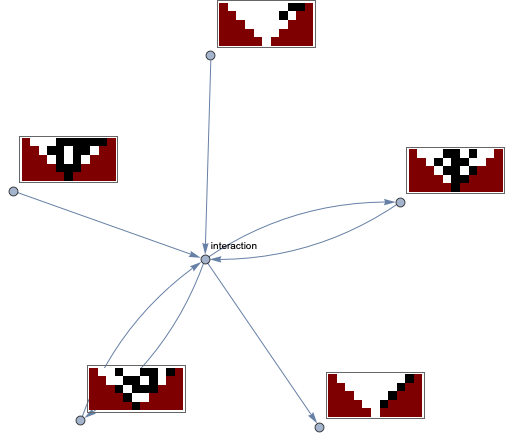
Figure 5: A graph of the glider interactions
Once the gliders interactions have been catalogued, they are analyzed combinatorially for collisions with each other. These collisions are then separated into components with two inputs and two outputs similar to the logical gate format. Then, the system cycles through the final gliders which could be used to replace the {A,D} and {C, B} gliders in the glider configured logical gate. If a configuration is found in which the all four variables A,B,C,D are filled similarly to the exact configuration of the Nand gate, that configuration is regarded to be universal.