Mike,

WL is a commonly used acronym for Wolfram Language.

The equation you are trying to find the roots of is a quartic polynomial. So there are four solutions some of which may be degenerate. If you expand and re-arrange

$$a^4-9 a^3+26 a^2-24 a-960=0$$

eq1 = Expand[a (a - 2) (a - 3) (a - 4)] - 960 == 0
(* -960 - 24 a + 26 a^2 - 9 a^3 + a^4 == 0 *)

Factoring yields one root, a = 8.

Factor@eq1
(* (-8 + a) (120 + 18 a - a^2 + a^3) == 0 *)

The remaining cubic has three roots, one real a = -3.53019 and two complex (which are conjugate) a = 2.2651 - 5.37232 I and a = 2.2651 + 5.37232 I

You can visualize the real roots by plotting the function

Plot[Evaluate@First@eq1, {a, -5, 10}]

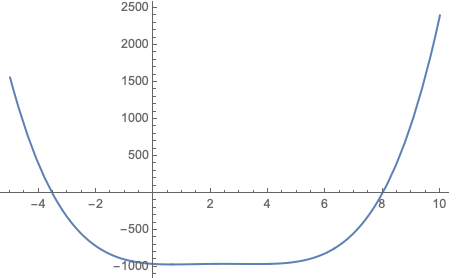
If you are interested in just integer or real roots you can add a region specification to Solve

Solve[eq1, a \[Element] Integers]
(* {{a -> 8}} *)

Solve[eq1, a \[Element] Reals] // N
(* {{a -> 8.}, {a -> -3.53019}} *)

Hope that helps.

Rohit.... Thanks a million for that!!! It helped me enormously. Fabulous reply, and I am greatly indebted to you...... thanks, and thanks, and thanks! :-) "-)

regards, Mike

Hi Mike,

Using WL

Solve[960 == a (a - 2) (a - 3) (a - 4), a] // N
(* {{a -> 8.}, {a -> -3.53019}, {a -> 2.2651 - 5.37232 I}, {a -> 
   2.2651 + 5.37232 I}} *)