Yes to the first question. It was just a test, where I took a number and turned it into exponent operations (with no multiplications between different numbers in that attempt). For some numbers this should be shorter and others should not change much. In the example: 10^7+47=10000047 it gets smaller (gets smaller but do not know much about less "bits "). I believe it depends a lot on the initial number... It is true that the number 2855754796332=1300^4-51^5-178417 (in this possible form) also did not get smaller, perhaps if slightly changing the method (adding multiplications to the method like "a.b^c+d.e^f+g" instead of only exponents “b^c+e^f+g” as I did..) or some other values in the code...don't know... After all it was just a try.

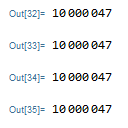
I did some tests but I don't know if this will be useful to you.. I did with smaller numbers and with more than 3 “parts” as you would like, but it may be an idea...Example for a more obvious number: 10000047

s = 10000047;
w = Flatten@
  ParallelTable[{If[Abs[m^n - s] < 1000000, {m, n}, {}], 
    If[Abs[m^n - s] < 1000000, (-1)*(m^n - s), {}]}, {m, 2, 50}, {n, 
    2, 50}]; w

..then continuing successively in the first example:

s = 234422;
w = Flatten@
  ParallelTable[{If[Abs[m^n - s] < 1000, {m, n}, {}], 
    If[Abs[m^n - s] < 1000, (-1)*(m^n - s), {}]}, {m, 2, 50}, {n, 2, 
    50}]; w

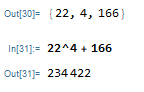
..and so on for all values and regulating the numbers within the code until you get to the following table:

5^10 + 22^4 + 13^2 - 3
6^9 - 5^7 + 2^9 - 6^2
10^7 + 7^2 - 2
25^5 + 22^4 + 13^2 - 3

It is clear that this method does not cover all possibilities, but at least arrives at some result. It is susceptible to the values chosen within the code and the processing speed for larger numbers!

In the case of a larger and less obvious number for example: 2855754796332

s = 2855754796332;
w2 = Flatten@
  ParallelTable[{If[Abs[m^n - s] < 1000000000, {m, n}, {}], 
    If[Abs[m^n - s] < 1000000000, (-1)*(m^n - s), {}]}, {m, 2, 
    2000}, {n, 2, 2000}]; w2

...and doing the same procedure by modifying the code values until you simplify the result:

s = 345203668;
w3 = Flatten@
  ParallelTable[{If[Abs[m^n - s] < 1000000, {m, n}, {}], 
    If[Abs[m^n - s] < 1000000, (-1)*(m^n - s), {}]}, {m, 2, 400}, {n, 
    2, 400}]; w3

..and so it continues until it reaches the final result (at least the result I found):

1300^4 - 51^5 - 3^11 - 6^4 + 5^2 + 1

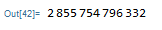
These were my tests but the numbers were not so big and the modifications to the code at every step were done manually. So, for much larger numbers this method would give a little more work.

There may be another method to do that, or even some way to have fewer terms, but I don't know..

Even if it's not exactly what you'd like, it might be of some use.

Yes, I have a reason to believe it.

8^13=549755813888

And if I want to tweak the result:

8^13+8=549755813896

" "Maybe some sort of exponential greedy-wise" perhaps you have already read the algorithm and are waiting for others to respond knowing it for some reason? Yes there are many algorithms involving exponent number representation - the best are patented and on the Intel chip i assume. " No but go ahead, I'm waiting to hear another way. I'm still searching too... If 9^9=387420490 ( which it does ) and I want 397361144 then that is one step there, however it does leave a whopping 9940654 remaining. We must be doing it wrong...

What is: 36^^3973g9f3igvh4a6e3o60cz93y96 == 94728228010056348223853483453583434753322 ? How did you get that smaller number at left? And why is there 2 '^'?