Why not to start from stripped down simple version and get it to work first, then built from it and add things like various potentials, constants, Input, etc. Here is a start.
L = 30; T = 20;
sol = NDSolve[{I D[u[t, x], t] + D[u[t, x], x, x] - Abs[x] u[t, x] == 0,
u[0, x] == Sech[x] Exp[I x], u[t, -L] == u[t, L]}, u, {t, 0, T}, {x, -L, L}];
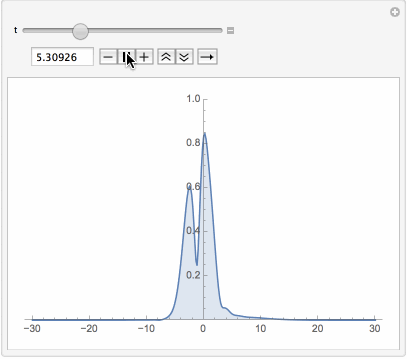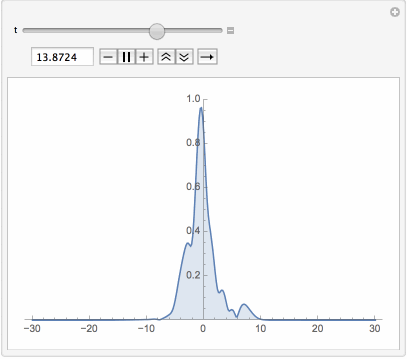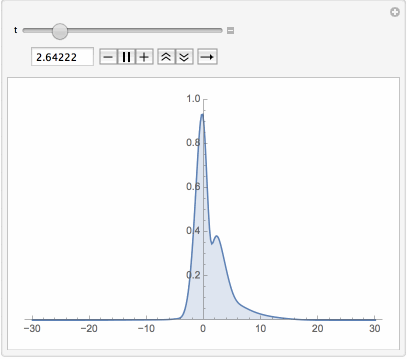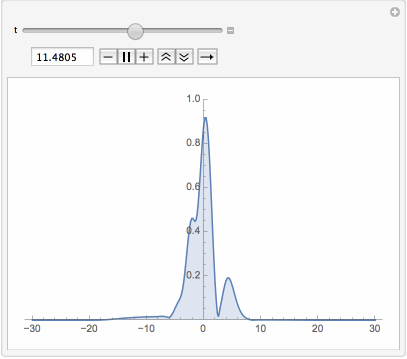
Manipulate[Plot[Evaluate[Abs[u[t, x] /. First[sol]]], {x, -L, L},
PlotPoints -> 40, PlotRange -> {0, 1}, Filling -> Bottom], {t, 0, T}]
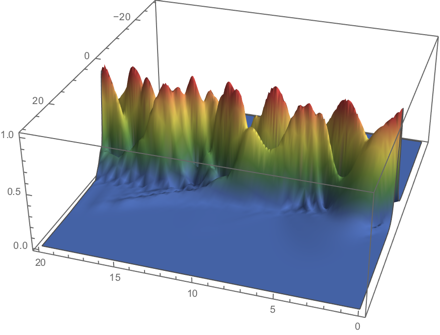
Plot3D[Evaluate[Abs[u[t, x] /. First[sol]]], {t, 0, T}, {x, -L, L},
PlotPoints -> 60, Mesh -> None, PlotRange -> All, ColorFunction -> "DarkRainbow"]
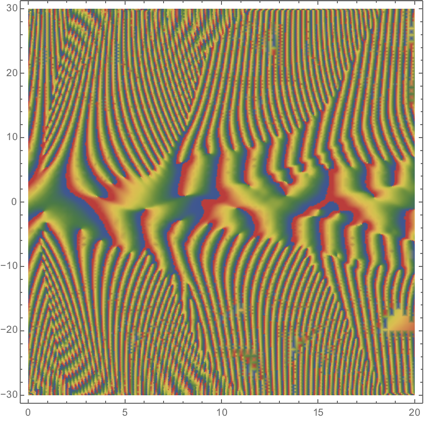
DensityPlot[Evaluate[Arg[u[t, x] /. First[sol]]], {t, 0, T}, {x, -L, L},
PlotPoints -> 60, MaxRecursion -> 3, ColorFunction -> "DarkRainbow"]