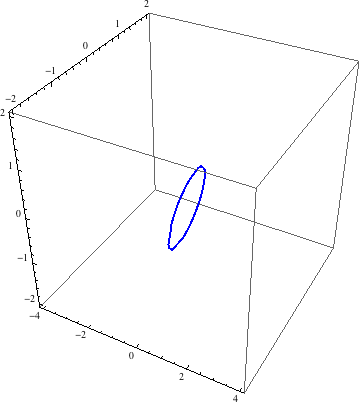
If by surfaces you mean where each formula is zero, then it turns out that
13x^2+40y^2+4z^2+28xy-8xz-8yz-x+y+z+1 = 0 has no real solutions. Substituting another formula, here is a way.
ContourPlot3D[{13 x^2 + 8 y^2 + 4 z^2 + 2 x y - 8 x z - 8 y z - x +
y + z - 1, x - y + z}, {x, -4, 4}, {y, -2, 2}, {z, -2, 2},
Contours -> {0}, ContourStyle -> None, Mesh -> None,
BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Thick, Blue}}}]