To answer this question, we can compare two methods for solving the heat equation: 1) the "MethodOfLines" in which boundary condition Derivative[1, 0][u][5, t] == -h (u[5, t] - u1) is used; and 2) FEM in which boundary condition NeumannValue[-h (u[x, t] - u1), x == 5] is used.
eq = D[u[x, t], t] - D[u[x, t], x, x];
ic = u[x, 0] == 0;
bc = {u[0, t] == 0,
Derivative[1, 0][u][5, t] == -h (u[5, t] - u1) (1 - Exp[-10 t])};
bcn = DirichletCondition[u[x, t] == 0, x == 0];
h = 2; u1 = 2.5;
sol = NDSolveValue[Flatten[{eq == 0, ic, bc}],
u, {t, 0, 5}, {x, 0, 5},
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid",
"MinPoints" -> 100, "MaxPoints" -> 100, "DifferenceOrder" -> 4}}]
Needs["NDSolve`FEM`"];
mesh = ToElementMesh[ImplicitRegion[0 <= x <= 5, {x}],
"MaxCellMeasure" -> 0.001];
solN = NDSolveValue[
Flatten[{eq == NeumannValue[-h (u[x, t] - u1), x == 5], ic, bcn}],
u, {t, 0, 5}, x \[Element] mesh,
Method -> {"FiniteElement",
"MeshOptions" -> {"MaxCellMeasure" -> 0.001}}]
Comparing the two solutions in Fig. 1, we see their identity
{Plot3D[sol[x, t], {t, 0, 5}, {x, 0, 5}, Mesh -> None,
ColorFunction -> Hue, AxesLabel -> Automatic,
PlotLabel -> "Method Of Lines"],
Plot3D[solN[x, t], {t, 0, 5}, {x, 0, 5}, Mesh -> None,
ColorFunction -> Hue, PlotRange -> All, AxesLabel -> Automatic,
PlotLabel -> "Finite Element"]}
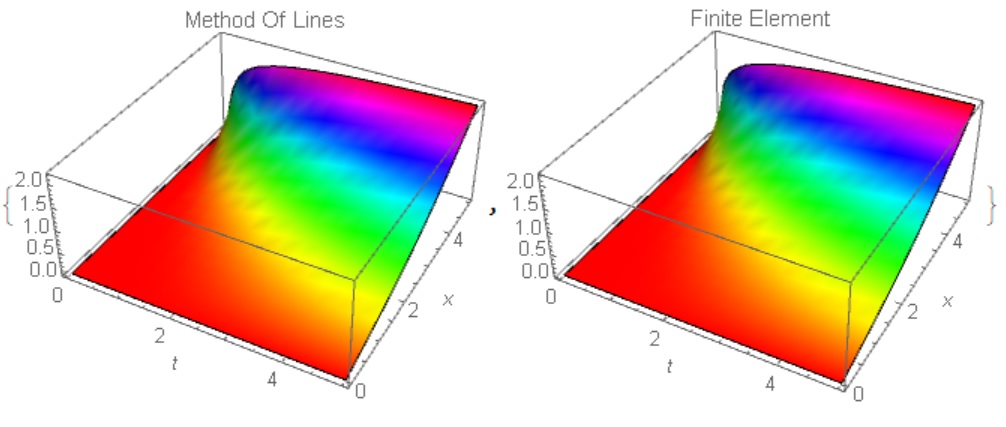
Note that in the Method Of Lines a damping factor is used to agree on the initial and boundary conditions (1 - Exp[-10 t]).