Hi, I'm have been trying, unsuccessfully, to solve the following define integral:

Using the Jacobi-Anger expansion and the assumptions shown above this integral should have the following closed-form:

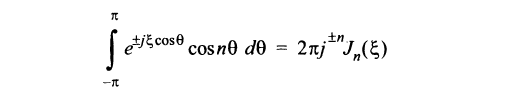
Can anyone please tell me if I'm having any error in the Mathematica input?

Attached you can find the Mathematica input that I'm using to solve this integral.

Assuming[{Constant -> \[Xi], \[Theta] \[Element] Reals, 
   n \[Element] Integers}, \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-\[Pi]\), \(\[Pi]\)]\(
\*SuperscriptBox[\(E\), \(\(\ \)\(\[CapitalIota]\ \[Xi]\ \
Cos[\[Theta]]\)\)] Cos[
     n\ \[Theta]] \[DifferentialD]\[Theta]\)\)] // TraditionalForm