With the new Mathematica object "FindEquationalProof" it is possible to prove, that one expression in Boolean Logic is equal to the corresponding expression in Set Theory, despite the first is dealing with Booleans, the other is dealing with Sets (refer to the following example).
In[868]:= axioms = {
ForAll[{A, B},
union[A, intersection[B, complement[B, "\[CapitalOmega]"]]] == A],
ForAll[{a, b}, and[a, or[b, not[b]]] == a]};
hypoth = ForAll[{x, y},
and[x, or[y, not[y]]] ==
union[x, intersection[y, complement[y, "\[CapitalOmega]"]]]];
In[870]:= proof = FindEquationalProof[hypoth, axioms, TimeConstraint -> 10]
and here a hardcopy for better visualization: 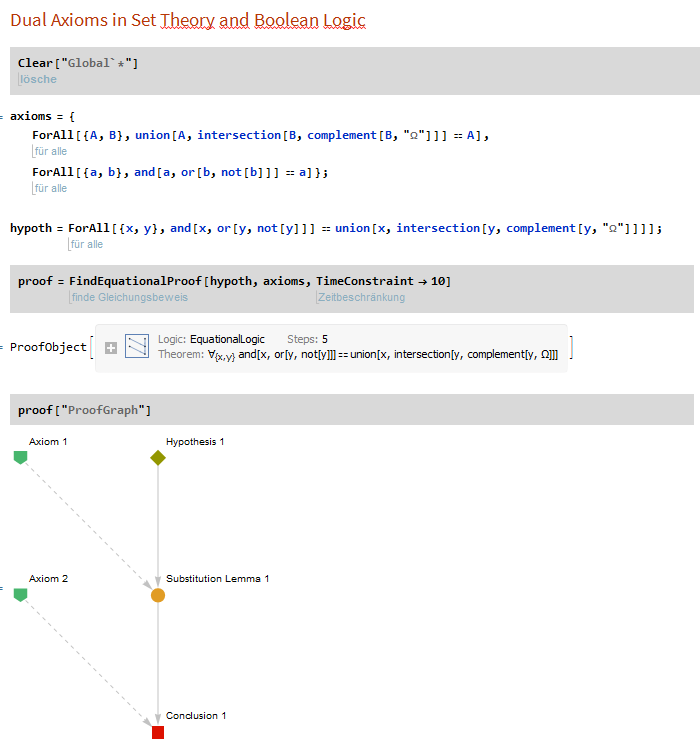
This should not be possible!
At the "MetaMath Proof Explorer Home Page" it is explained, why it is necessary to define "Distinct Variables" and to distinct variables between "wffs", "sets" and "classes", to perform proper mathematical proofs:
http://us.metamath.org/mpeuni/mmset.html
I wanted to implement some basic axiom systems for example Booleans and from Set Theory, but I got proofs, which are not really valid, so that I could not further use FindEquationalProof for my intention. I updated Mathematica to Release 12 particular due to my great expectations to this new functionality.
Is there any workarround, to prevent FindEquationalProof matching different symbols of different types ? Is there any hope to get FindEquationalProof improved, so that the implementation of axiom systems like shown at MetaMath will be possoble in the future? This would be a really great progress for me
Thank you for any comments
Regards Uwe