Factorio is a game where you crashed on a planet with your space-craft. You have to built a new rocket and leave this planet again. In order to do so you will need to mine metals and built yourself a factory, make labs to do research, and built machine that make other machines, and finally combine all of this to make rockets, satellites, rocket fuel, trains, flying robots, oil products, steam engines, plastics, electronic chips, iron, copper, uranium centrifuging, solar panels etc etc. An incredibly complicated game where the key idea is that you automate this entire process using machines in your factory.

See https://www.youtube.com/watch?v=KVvXv1Z6EY8 .

To do research you need to manufacture research-packs which are created from other resources, which might also be created from other resources etc. etc.

Here is some code that interprets the Factorio wiki:

baseurl = "https://wiki.factorio.com";
ClearAll[GetImage]
ClearAll[FindDependencies]
GetImage[url_] := GetImage[url] = Import[url]
FindDependencies[url_String] := 
 FindDependencies[url] = Module[{xml, c, end, other, sel = 1},
   xml = Import[url, "XMLObject"];
   c = Cases[xml, 
     XMLElement["table", {}, {contents_}] :> contents, \[Infinity]];
   c = Select[c, 
     MemberQ[#, XMLElement["p", {}, {"Recipe\n"}], \[Infinity]] &];
   c = FirstCase[#, 
       XMLElement[
         "tr", {}, {XMLElement[
           "td", {___, 
            "class" -> "infobox-vrow-value"}, {x__}]}] :> {x}, 
       Missing[], \[Infinity]] & /@ c;
   If[Length[c] > 0,
    c = c[[sel]];
    c = Cases[c, 
      XMLElement[
        "div", {"class" -> "factorio-icon", 
         "style" -> "background-color:#999;"}, {XMLElement[
          "a", {"shape" -> "rect", "href" -> hrefurl_, 
           "title" -> name_}, {XMLElement[
            "img", {"alt" -> _, "src" -> imgurl_, "width" -> "32", 
             "height" -> "32",___}, {}]}], 
         XMLElement[
          "div", {"class" -> "factorio-icon-text"}, {num_}]}] :> 
       FactorioObject[baseurl <> hrefurl, name, 
        GetImage[baseurl <> imgurl], 
        ToExpression@StringTrim[StringReplace[num, "k" -> "000"]]], \[Infinity]];

    c = DeleteCases[c, FactorioObject[_, "Time", _, _]];
    {{end}, other} = TakeDrop[c, -1];
    other -> end,
    {}
    ]
   ]
ClearAll[FindDependencyTree]
FindDependencyTree[url_String, iterations_: 6] := 
 Module[{a, known, unknown, new, vlbls, vertices},
  a = FindDependencies[url];
  known = {a};
  Do[
   unknown = Join @@ known[[All, 1]];
   unknown = DeleteDuplicates[Complement[unknown, known[[All, 2]]]];
   new = DeleteDuplicates[FindDependencies@*First /@ unknown];
   new = DeleteCases[new, {}];
   known = DeleteDuplicates[Join[known, new]];
   ,
   {iterations}
   ];
  vlbls = 
   Cases[known, 
    FactorioObject[_, name_, 
      icon_, _] :> (name -> 
       Image[icon, ImageSize -> 32]), \[Infinity]];
  vertices = 
   DeleteDuplicates[
    Join @@ Table[(# -> k[[2, 2]]) & /@ k[[1, All, 2]], {k, known}]];
  <|"LabelRules" -> vlbls, "Vertices" -> vertices, 
   "Dependencies" -> known|>
  ]

Let's ask the dependency tree for the first science pack:

out1 = FindDependencyTree["https://wiki.factorio.com/Science_pack_1"];
Graph[out1["Vertices"], VertexShape -> out1["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]

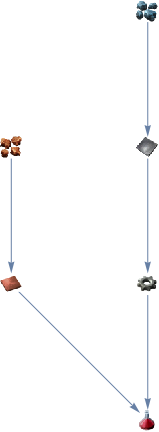
To make Science pack 1, we need gears and copper plates. And to make gears we need iron plates. The iron and copper plates are made from iron and copper ore.

This is still relatively simple, let's look at the other science packs:

out2 = FindDependencyTree[
   "https://wiki.factorio.com/Science_pack_2"];
Graph[out2["Vertices"], VertexShape -> out2["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]
out3 = FindDependencyTree[
   "https://wiki.factorio.com/Science_pack_3"];
Graph[out3["Vertices"], VertexShape -> out3["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]
out4 = FindDependencyTree[
   "https://wiki.factorio.com/Military_science_pack"];
Graph[out4["Vertices"], VertexShape -> out4["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]
out5 = FindDependencyTree[
   "https://wiki.factorio.com/Production_science_pack"];
Graph[out5["Vertices"], VertexShape -> out5["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]
out6 = FindDependencyTree[
   "https://wiki.factorio.com/High_tech_science_pack"];
Graph[out6["Vertices"], VertexShape -> out6["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]

Resulting in:

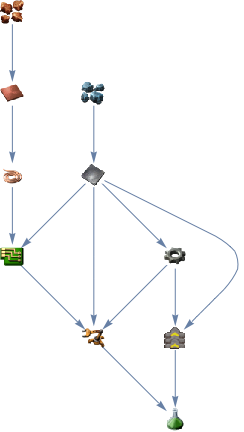
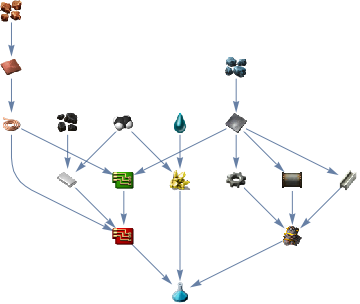
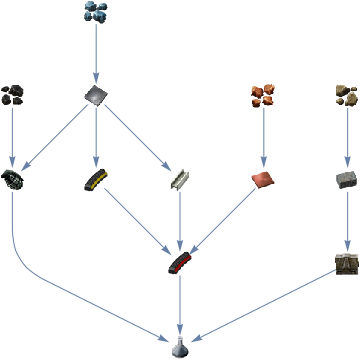
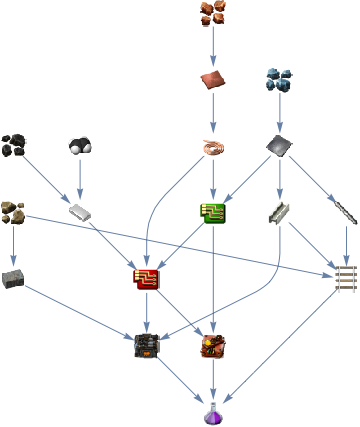
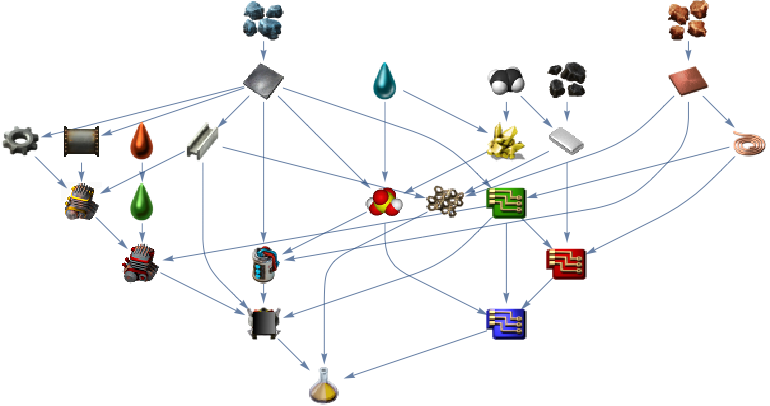
To summarize, let's combine all the graphs:

o = {out1, out2, out3, out4, out5, out6};
Graph[Union @@ o[[All, "Vertices"]], 
 VertexShape -> Union @@ o[[All, "LabelRules"]], 
 VertexSize -> {"Scaled", 0.02}, ImageSize -> 1000, 
 AspectRatio -> 1/GoldenRatio]

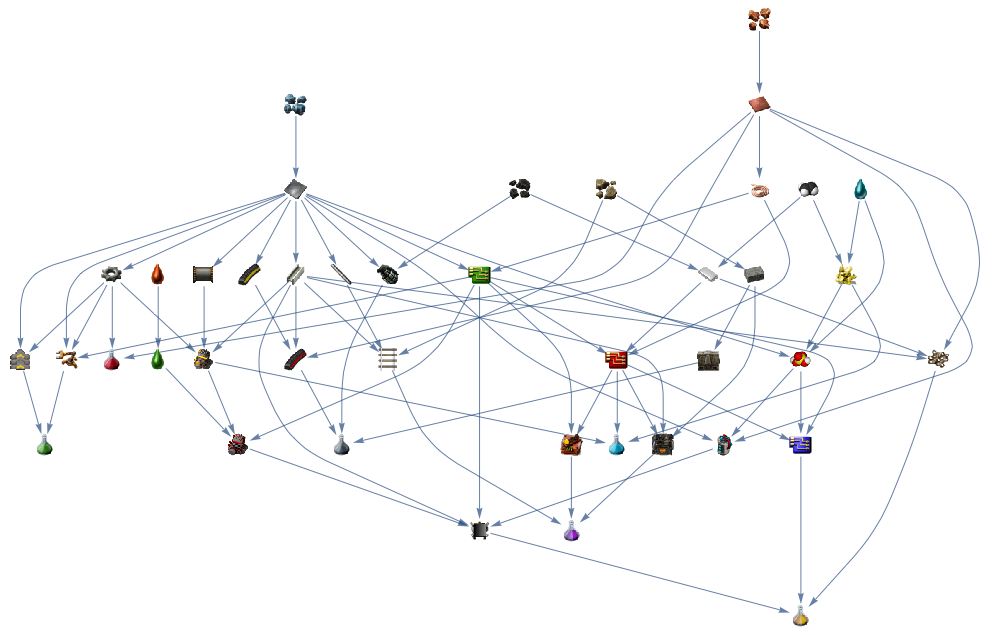
As you can see the dependencies are very complex to get all the research packs. Of course there are many things you need to create with your machines, think of transport belts, trains, mining, steam generation, and energy production, water and other chemicals etc etc.

One of the most expensive parts is a satellite (to guide your rocket):

out = FindDependencyTree["https://wiki.factorio.com/Satellite"];
Graph[out["Vertices"], VertexShape -> out["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]

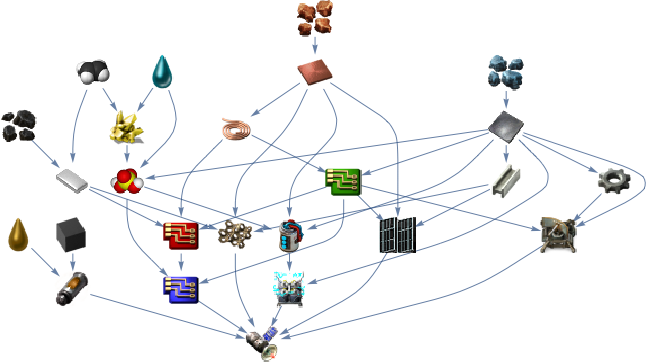
I hope you like this little exploration on Graphs and Factorio. We could also use Mathematica's Graph technology to design balanced belt splitter designs: http://i.imgur.com/tz2Jc3p.png ! I will leave that for some other time. For now, explore the different buildings or parts, for example have a look at the rocket silo:

out = FindDependencyTree["https://wiki.factorio.com/Rocket_silo"];
Graph[out["Vertices"], VertexShape -> out["LabelRules"], 
 VertexSize -> {"Scaled", 0.05}]

If you haven't played already… be careful… it is an incredibly addicting game!