This can be used as a regular analytical solution, for example
s = DSolve[{i[t] == Cr vc'[t],
vc[t] == vco[t] (1 + m) - Lr i'[t], -(1 + m) i[t] - vco[t]/RL ==
Co vco'[t], vc[0] == Vcrmax, i[0] == 0, vco[0] == Vo}, {i, vc,
vco}, t];
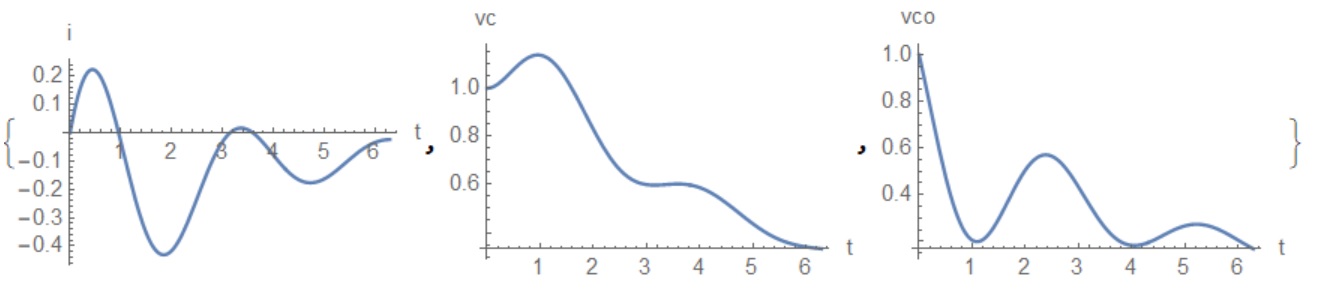
{Plot[Evaluate[
i[t] /. s[[1, 1]] /. {Cr -> 1, Lr -> 1, m -> 1, Co -> 1, RL -> 1,
Vcrmax -> 1, Vo -> 1}], {t, 0, 2 Pi}, AxesLabel -> {"t", "i"}],
Plot[Evaluate[
vc[t] /. s[[1, 2]] /. {Cr -> 1, Lr -> 1, m -> 1, Co -> 1, RL -> 1,
Vcrmax -> 1, Vo -> 1}], {t, 0, 2 Pi}, AxesLabel -> {"t", "vc"}],
Plot[Evaluate[
vco[t] /. s[[1, 3]] /. {Cr -> 1, Lr -> 1, m -> 1, Co -> 1, RL -> 1,
Vcrmax -> 1, Vo -> 1}], {t, 0, 2 Pi},
AxesLabel -> {"t", "vco"}]}