As a sort of addendum to Jofre's lovely excursion into pumpkin-adjacent miscellanea, here's a parametric equation I made up a number of years ago to simulate a pumpkin:
With[{p = 1, r = 1/20, b = 2/3},
ParametricPlot3D[Append[((p + r) {Cos[u], Sin[u]} -
r Exp[-v^2] Through[{Cos, Sin}[(p + r) u/r]])
b^2 Cos[v], b Sin[v]]/(b^2 Cos[v]^2 + Sin[v]^2),
{u, 0, 2 ?}, {v, -?/2, ?/2}, Exclusions -> None,
Lighting -> "Neutral", Mesh -> None, PlotPoints -> 75,
PlotStyle -> Directive[Orange, Specularity[1, 20]]]]

(You can add a stem yourself, if you wish.)
The observant will notice that the surface was built-up from a hippopede and an epicycloid.
For the chemically minded, there is a family of molecules whimsically named the cucurbiturils, in part because the shape of these molecules reminded their discoverers of a pumpkin. As the default rendering done by Molecule[]/MoleculePlot3D[] from the molecule's SMILES string leaves something to be desired, I'll instead import the model featured on the Molecule of the Month webpage:
MoleculePlot3D[Import["http://www.chm.bris.ac.uk/motm/cucurbituril/cucurbituril.mol"]]
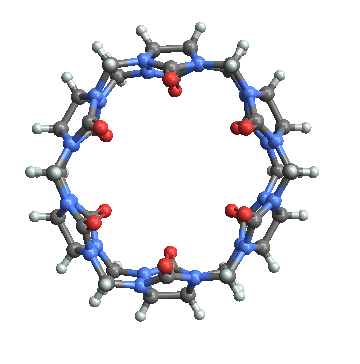
This particular member is called cucurbit[6]uril, as there are six glycoluril units involved in the assembly. Higher and lower oligomers of it are known.
(As an aside, the molecule featured in the MoleculeViewer home page is a lower oligomer, cucurbit[5]uril.)