Hi, I am trying to make a digital version of a toy that I had as a kid, which I hope will help teach my 6-year old daughter about place values in arithmetic.
I am pretty new to Mathematica, although I used it some 10 years ago, so I hope that someone here can easily spot the flaw in my program.
The toy I am trying to re-create was basically a stripped down version of a pascaline, Pascal's calculator. The one I had was very simple, with 4 digits and 4 buttons. To make the number 43, you could press the 10's button 4 times and the 1's button 3 times (or you could press the 1's button 43 times, etc). Then to add, say 59, you could press the 10's button 5 times and the 1's button 9 times. The machine did the carrying for you. It didn't subtract.
I am able to get something similar to work, but I can't figure out how to animate the numbers rolling, which I think is kind of crucial...seeing the 9's roll over into 10's. I have been able to roll the digits of a simple counter, but not once I put in the buttons to "add 10", etc.
I have an image of the digits i want to use here:
horizTallyDigits=

htdigits = Flatten@ImagePartition[horizTallyDigits, {17, 26}];
tallydigits[n_] := ImageAssemble[List /@ RotateLeft[htdigits, n]];
(* and write functions to display any number, eg. 4.5 shows the wheel \
half way between 4 and 5 *)
window[x_] := (n = IntegerPart[x]; f = Round[26 (x - n)];
ImageTake[
tallydigits[Mod[n, 10]], {f, If[f > 0, 28, 29] + f}, {1, 17}]);
This works fine, and I can see the numbers roll as I would like (eg with a Trigger). But I want the numbers to roll in response to button presses. So I create buttons and variables that keep track of where the wheels are. I have the buttons generate an Animation List, but it seems to wait for that to finish before updating the image.
I've tried putting the Dynamic in lots of different places...some places make the counters roll very fast and never stop, others don't update at all. I haven't figured out a way to make it update the way I would like. I'm clearly missing something.
(* I want a device where when i click the +10 button, i see the 10's \
digit moving up slowly. if it's a 9, then it will also cause the \
100's digit to move with it *)
pascalineTotal = 0; pascalineButtons = {0, 0, 0, 0};
Clear[pascaline]; Clear[animlist]; Clear[newCounter];
newCounter[xvals_] := ImageAssemble[{window /@ xvals}];
animlist[lis_, change_, nsteps_] :=
(chg = change;
Do[If[(chg[[i]] > 0) || (chg[[i + 1]] > 0 && (lis[[i + 1]] == 9)),
chg[[i]] = 1], {i, Length[lis] - 1}];
fparts = Array[Mod[#1/nsteps, 10] &, nsteps];
lis + chg # & /@ fparts);
pascaline := (
al = animlist[IntegerDigits[pascalineTotal, 10, 4],
pascalineButtons, 20];
a = ListAnimate[newCounter[#] & /@ al, 5,
AnimationRepetitions -> 1];
pascalineTotal += FromDigits[pascalineButtons];
pascalineButtons = {0, 0, 0, 0} ; a)
(* This almost works, but it doesn't show the digits moving. The animate list is ignored until it is finished. I don't know why, related to Dynamic? *)
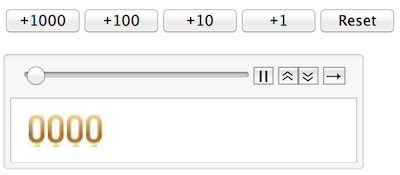
Row[{Button["+1000", (pascalineButtons = IntegerDigits[1000])],
Button["+100", pascalineButtons = IntegerDigits[100, 10, 4]],
Button["+10", pascalineButtons = {0, 0, 1, 0}],
Button["+1", pascalineButtons = {0, 0, 0, 1}],
Button["Reset", (pascalineTotal = 0;
pascalineButtons = {0, 0, 0, 0})]}]
Dynamic[pascaline]
Thanks,