There seem to be multiple ways to search for twin primes so that there are multiple routes to climb the same mountain. This time, we will introduce the search for twin primes using the sine function.

If positive integers are divided into prime numbers and composite numbers, the simple regularity is not visible in the appearance of prime numbers. However, the number of composites is clearly regular. Periodicity is easy to understand with regularity. That is why we use the sine function.

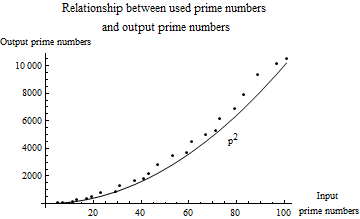
This time, we search for twin primes using sine functions and primes. You will get a twin prime that is the square of the largest prime used. However, there are conditions. The condition is that you know all the prime numbers between 5 and the maximum prime number. The following graph illustrates this.

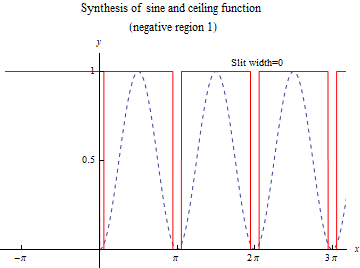
Use the sine function in combination with the ceiling function. The negative area of the sine function is 1. The positive area is composed of a sine function and a ceiling function as shown in the following figure. Square the sine function to avoid negative values. Sine functions with different periods, which are necessary during the search process, are added one after another. The size of the required prime number is determined by the size of the twin prime number to be searched. The required prime number is determined automatically.

We used prime numbers greater than $5$, and set ${\rm Prime} [999999999999]$ as the upper limit (if it is too large, it takes too much time and is not practical). The prime number to be used is generated by ${\rm Prime} [pn]$ of ${\rm Mathematica}\, (pn = 3,4,5 ?)$. The maximum $n$ specified in the search is written as $nmax$, and the maximum prime number required is $pnmax$ = $0.7835 \times (nmax) ^ {0.7656} $+ $5$. (I couldn't write $n_{max}$ in the sentence so I decided to "$nmax$")

In other words, nend is $n_{max}$, and the prime number $pn_{max}=0.7835 \times\;(n_{max})^{0.7656}+5 $.

The twin prime number is determined by the following three equations.

$$\begin{eqnarray} f_1(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2-7}{6}\right)\right\} \tag{1a}\\ f_2(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2+2p-5}{6}\right)\right\} \tag{1b}\\ f_3(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2+4p-5}{6}\right)\right\} \tag{1c}\\ \end{eqnarray}$$

$$\begin{align*} &n=1,2,3\cdots \\ &p:\text {Prime number greater than 5 ($5,7,11\cdots$)}\\ &\text {However, a negative region in {} is 1.}\\ \end{align*} $$

A prime number of type ( $6n + 1$) is determined by equation ( $1a$), and a prime number of type ( $6n-1$) is determined by equations ( $1b$) and ( $1c$). I feel asymmetric here too, but is this essential? Or is it just caused by asymmetry due to my handling? Aside from that, the twin prime number is determined by three equations ( $1$). The equation ( $1$) is processed by the ceiling function, and the product is taken as shown in the equation ( $2$).

$$ nt=\prod{p=5}^{p{max}} \left(\lceil f1\rceil\times\lceil f2\rceil\times\lceil f3\rceil\right )\times n \tag{2}\ $$

$$\begin{align*} &\lceil f_1\rceil,\lceil f_2\rceil,\lceil f_3 \rceil: \text {Ceiling function of equation (1).}\\ &n=1,2,3\cdots \\ &n_t:\text {Integer that is a twin prime in equation (3).}\\ &p:\text {Prime number greater than 5 ($5,7,11\cdots$)}\\ &p_{max}:\text {Maximum prime number determined by $n_{max}$. (=Prime[$pn_{max}$])}\\ &pn_{max}=0.7838\times(n_{max})^{0.7656}+5?\text {was used.} \end{align*}$$

Using $n_t$, the twin prime is given by equation ( $3$).

$$\begin{equation} {\rm Twin\ prime}= \left \{ \begin{array}{l} (6n_t-1)+6 \\ (6n_t+1)+6 \end{array} \right.\tag{3} \end{equation} $$

$$\begin{align*} n_t:\text {Integer obtained from equation (2).}\\ \end{align*} $$

The program is shown below. The start of the search is indicated by “${\rm nstart} $”, and the end is indicated by “${\rm nend}$”.

nstart = 1;
nend = 100;

"***************************************************************";
func1[n_] := 
  If[If[n - (Prime[pn]^2 - 7)/6 < 0, 1, 
     Ceiling[(Sin[(2*Pi/Prime[pn])*(n - (Prime[pn]^2 - 7)/6)])^2]] == 
    1, 1, 0];

func2[n_] :=
  If[If[n - (Prime[pn]^2 + 2*Prime[pn] - 5)/6 < 0, 1,
     Ceiling[(Sin[(2*
            Pi/Prime[pn])*(n - (Prime[pn]^2 + 2*Prime[pn] - 5)/
             6)])^2]] == 1, 1, 0];

func3[n_] :=
  If[If[n - (Prime[pn]^2 + 4*Prime[pn] - 5)/6 < 0, 1,
     Ceiling[(Sin[(2*
            Pi/Prime[pn])*(n - (Prime[pn]^2 + 4*Prime[pn] - 5)/
             6)])^2]] == 1, 1, 0];

Clear[nt];
n = nstart;
pnmax = IntegerPart[0.7835*nend^0.7656] + 5;
Print["====== The calculation results are shown below. ======"];
Print["nstart= ", nstart];
Print["nend= ", nend];
Print["---------"];

If[nstart > 0 && nend > 0 && nend > nstart && pnmax <= 999999999999,
  Do[
   If[Product[func1[n]*func2[n]*func3[n], {pn, 3, pnmax}] == 1, 
     nt = n, nt = 0]

    If[nt > 0, Print["nt= ", nt]];
   If[nt > 0, Print["Twin prime= ", {6*nt + 5, 6*nt + 7}]];

   If[nt > 0, 
    Print["PrimeQ[(1),(2)]= ", {PrimeQ[6*nt + 5], PrimeQ[6*nt + 7]}]];

   If[n == nend, Break[]], {n, nstart, nend}], 
  Print["===! The conditions are not met.==="]];

This is an example of ${\rm nstart }= 1$ and ${\rm nend} = 100$. The calculation result is as follows.

====== The calculation results are shown below. ======
nstart= 1
nend= 100
---------

nt= 1
Twin prime= {11,13}
PrimeQ[(1),(2)]= {True,True}

nt= 2
Twin prime= {17,19}
PrimeQ[(1),(2)]= {True,True}

nt= 4
Twin prime= {29,31}
PrimeQ[(1),(2)]= {True,True}

nt= 6
Twin prime= {41,43}
PrimeQ[(1),(2)]= {True,True}

nt= 9
Twin prime= {59,61}
PrimeQ[(1),(2)]= {True,True}

nt= 11
Twin prime= {71,73}
PrimeQ[(1),(2)]= {True,True}

nt= 16
Twin prime= {101,103}
PrimeQ[(1),(2)]= {True,True}

nt= 17
Twin prime= {107,109}
PrimeQ[(1),(2)]= {True,True}

nt= 22
Twin prime= {137,139}
PrimeQ[(1),(2)]= {True,True}

nt= 24
Twin prime= {149,151}
PrimeQ[(1),(2)]= {True,True}

nt= 29
Twin prime= {179,181}
PrimeQ[(1),(2)]= {True,True}

nt= 31
Twin prime= {191,193}
PrimeQ[(1),(2)]= {True,True}

nt= 32
Twin prime= {197,199}
PrimeQ[(1),(2)]= {True,True}

nt= 37
Twin prime= {227,229}
PrimeQ[(1),(2)]= {True,True}

nt= 39
Twin prime= {239,241}
PrimeQ[(1),(2)]= {True,True}

nt= 44
Twin prime= {269,271}
PrimeQ[(1),(2)]= {True,True}

nt= 46
Twin prime= {281,283}
PrimeQ[(1),(2)]= {True,True}

nt= 51
Twin prime= {311,313}
PrimeQ[(1),(2)]= {True,True}

nt= 57
Twin prime= {347,349}
PrimeQ[(1),(2)]= {True,True}

nt= 69
Twin prime= {419,421}
PrimeQ[(1),(2)]= {True,True}

nt= 71
Twin prime= {431,433}
PrimeQ[(1),(2)]= {True,True}

nt= 76
Twin prime= {461,463}
PrimeQ[(1),(2)]= {True,True}

nt= 86
Twin prime= {521,523}
PrimeQ[(1),(2)]= {True,True}

nt= 94
Twin prime= {569,571}
PrimeQ[(1),(2)]= {True,True}

nt= 99
Twin prime= {599,601}
PrimeQ[(1),(2)]= {True,True}

First “${\rm nstart} $” and “${\rm nend} $” are displayed. Next, the selected $nt$, twin prime number, and prime number judgment result are shown. All twin prime numbers that exist in the interval are shown.(Added blank lines for better visibility)

Let's search for a slightly larger twin prime. ${\rm nstart} = 100000000$ and ${\rm nend} = 100001000$ will do. It takes time to calculate. The results are shown in the table.

.

$$ {\rm Table}\,1\;\;{\rm Example\,of\, twin \,prime \,number \,search \,using \,sine \,function}\\ ?{\rm nstart}=100000000,\,{\rm nend}=100001000?$$

\begin{array}{|c|c|}\hline n_t&{\rm Twin \;prime}\\ \hline 100000002 &\text{{600000017, 600000019}} \\ 100000049 &\text{{600000299, 600000301}} \\ 100000067 &\text{{600000407, 600000409}}\\ 100000126 &\text{{600000761, 600000763}}\\ 100000134 &\text{{600000809, 600000811}}\\ 100000267 &\text{{600001607, 600001609}} \\ 100000364 & \text{{600002189, 600002191}} \\ 100000401 & \text{{600002411, 600002413}} \\ 100000412 & \text{{600002477, 600002479}} \\ 100000452 & \text{{600002717, 600002719}} \\ 100000457 & \text{{600002747, 600002749}} \\ 100000464 & \text{{600002789, 600002791}} \\ 100000494 & \text{{600002969, 600002971}} \\ 100000589 & \text{{600003539, 600003541}} \\ 100000676 & \text{{600004061, 600004063}} \\ 100000697 & \text{{600004187, 600004189}} \\ 100000767 & \text{{600004607, 600004609}} \\ 100000776 & \text{{600004661, 600004663}} \\ 100000841 & \text{{600005051, 600005053}} \\ 100000856 & \text{{600005141, 600005143}} \\ 100000874 & \text{{600005249, 600005251}} \\ 100000896 & \text{{600005381, 600005383}} \\ 100000996 & \text{{600005981, 600005983}} \\ \hline \end{array}