Group Abstract Group Abstract

Message Boards Message Boards

2
|
5.6K Views
|
2 Replies
|
5 Total Likes
View groups...
Share
Share this post:

Calculating a polygon and its center coordinate from an Ellipsoid Arc

cray co
Posted 6 years ago

Hi everyone! I have an interesting challenge that it out of my competency and thus I would need some help to figure out how to do this.

We receive data like this: Ellipsoid Arc: LatSign=North,Lat=45.530060 degrees,Long=-73.547783 degrees,InnerRadius=245 meters,UncertaintyRadius=190 meters,OffsetAngle=268 ,IncludedAngle=22 degrees,Confidence=0

and would like to determine the resulting polygon (green) and center (red) like this example: Elllipsoid Arc result

We're looking at implementing the solution in python. Here some reference to help: https://www.engineering.com/Library/ArticlesPage/tabid/85/articleType/ArticleView/articleId/109/Centroids-of-Common-Shapes.aspx https://en.wikipedia.org/wiki/Centroid#By_geometric_decomposition

All help would be greatly appreciated
POSTED BY: cray co
2 Replies
Sort By:
Rohit Namjoshi
Rohit Namjoshi
Posted 6 years ago

Hi cray co,

This uses the centroid of the sector rather than the mean angle/radius used in @Henrik Schachner 's solution. As expected, the two results are slightly different. The "right" answer depends on your requirements.

center = GeoPosition[{45.530060, -73.547783}];
innerRadius = 245; uncertaintyRadius = 190;
angleRange = {268, (268 + 22)};
outer = GeoDisk[center, innerRadius + uncertaintyRadius, angleRange];
inner = GeoDisk[center, innerRadius, angleRange];

{innerPoints, outerPoints} = 
  Cases[GeoGraphics[#], _Polygon, Infinity] & /* Last /* Last /@ {inner, outer};

{innerPoints, outerPoints} = (GeoPosition[
       GeoGridPosition[#, "Mercator", "ITRF00"]])[[1]] & /@ {innerPoints, outerPoints};

{innerRegion, outerRegion} = 
  DiscretizeGraphics /@ {Polygon@innerPoints, Polygon@outerPoints};

sector = RegionDifference[outerRegion, innerRegion];
centroid = RegionCentroid@sector;

GeoGraphics[{outer, inner, GeoMarker@GeoPosition@centroid}, ImageSize -> 700]

enter image description here

POSTED BY: Rohit Namjoshi

Here comes a first guess how this could be done - easily - in Wolfram Language:

pos = GeoPosition[{45.530060, -73.547783}];
rInner = Quantity[245, "Meters"];
rOuter = Quantity[245 + 190, "Meters"];
\[Phi]1 = 268 ;
\[Phi]2 = (268 + 22) ;
center = GeoDestination[pos, 
   GeoDisplacement[{Mean[{rInner, rOuter}], 
     Mean[{\[Phi]1, \[Phi]2}]}]];
GeoGraphics[{Thick, Red,
  GeoCircle[pos, rOuter, {\[Phi]1, \[Phi]2}],
  GeoCircle[pos, rInner, {\[Phi]2, \[Phi]1}],
  GeoPath[{GeoDestination[pos, GeoDisplacement[{rInner, \[Phi]1}]], 
    GeoDestination[pos, GeoDisplacement[{rOuter, \[Phi]1}]]}], 
  GeoPath[{GeoDestination[pos, GeoDisplacement[{rInner, \[Phi]2}]], 
    GeoDestination[pos, GeoDisplacement[{rOuter, \[Phi]2}]]}], 
  GeoMarker[center], pos}, ImageSize -> 700]

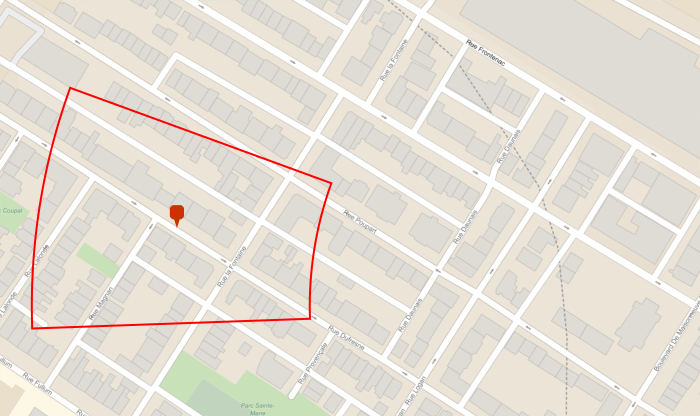
enter image description here

Isn't Mathematica just great ?!
POSTED BY: Henrik Schachner