Search for prime numbers greater than $11$ using sine functions and prime numbers. All prime numbers smaller than the square of the prime number used in the calculation are searched. For example, if you know that $5$ is a prime number, { $23,19,17,13,11$} below $25$ is calculated as a prime number. If you know that $23$ is a prime number, you can know a prime number { $523,521, ?$} of $529$ or less.

Prime numbers can be classified into two types. ( $6n-1$) type and ( $6n + 1$) type. This time we will search for {( $6n-1$) $+6$} and {( $6n + 1$) $ +6$} types, so we will search for prime numbers greater than $11$. Twin prime numbers are the same $n$, and ( $6n-1$) and ( $6n + 1$) are both prime numbers. If only one side of type ( $6n-1$) or ( $6n + 1$) is a prime number, it is a normal prime number. This time, the theme is a normal prime, that is, one of ( $6n-1$) or ( $6n + 1$) prime, but twin primes are also included in the solution.

Prime numbers can be determined by the three equations shown in ( $1$). Prime numbers of type ( $6n-1$) are determined by equations ( $1{\rm b}$) and ( $1{\rm c}$). The prime number of type ( $6n + 1$) is determined by equation ( $1{\rm a}$).

$$\begin{eqnarray} f_1(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2-7}{6}\right)\right\} \tag{1a}\\ f_2(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2+2p-5}{6}\right)\right\} \tag{1b}\\ f_3(n,p)&=&\sin^2\left\{\frac{2\pi}{p}\cdot\left(n-\frac{p^2+4p-5}{6}\right)\right\} \tag{1c}\\ \end{eqnarray}$$

$$\begin{align*} &n=1,2,3\cdots \\ &p:\text {Prime number greater than 5 ($5,7,11\cdots$)}\\ &\text {However, a negative region in {} is 1.}\\ \end{align*} $$

Use the sine function of equation ( $1$) in combination with the ceiling function. In the negative area of { } in the sine function, set $f (n, p) = 1$. (see the figure below)

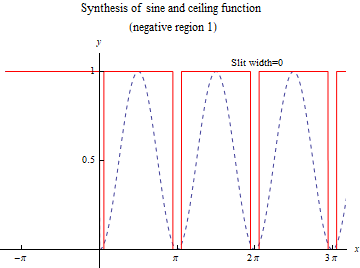
Next, take the prodct of $f (n, p)$ as shown in equation ( $2$). Equation ( $2{\rm a}$) corresponds to a prime number of type ( $6n-1$), and ( $2{\rm b}$) corresponds to a prime number of type ( $6n + 1$).

$$\begin{eqnarray} np_m&=&\prod_{p=5}^{p_{max}} \left(\lceil f_2\rceil \times\lceil f_3\rceil\right)\times n \tag{2a}\\ np_p&=&\prod_{p=5}^{p_{max}} \left(\lceil f_1\rceil \right)\times n \tag{2b}\\ \end{eqnarray}$$

$$\begin{align*} &\lceil f_1\rceil,\lceil f_2\rceil,\lceil f_3 \rceil: \text {Ceiling function of equation (1).}\\ &n=1,2,3\cdots \\ &n_t:\text {Integer that is a twin prime in equation (3).}\\ &p:\text {Prime number greater than 5 ($5,7,11\cdots$)}\\ &p_{max}:\text {Maximum prime number determined by $n_{max}$. (=Prime[$pn_{max}$])}\\ &pn_{max}=0.7838\times(n_{max})^{0.7656}+5?\text {was used.} \end{align*}$$

A prime number can be obtained by substituting $np _m$ and $np _p$ obtained in equation ( $2$) into equation ( $3$).

$$\begin{equation} {\rm Prime\ numbers}= \left \{ \begin{array}{l} (6\cdot np_m-1)+6 \\ (6\cdot np_p+1)+6 \end{array} \right.\tag{3} \end{equation} $$

$$\begin{align*} np_m,np_p:\text {Integer obtained from equation (2).}\\ \end{align*} $$

The search start number "${\rm nstart} $" and end number "${\rm nend}$" are given, and the program which searches the prime number which exists in the section is shown.

nstart = 1;
nend = 20;

"***************************************************************";
func1[n_] := 
  If[If[n - (Prime[pn]^2 - 7)/6 < 0, 1, 
     Ceiling[(Sin[(2*Pi/Prime[pn])*(n - (Prime[pn]^2 - 7)/6)])^2]] == 
    1, 1, 0];

func2[n_] :=
  If[If[n - (Prime[pn]^2 + 2*Prime[pn] - 5)/6 < 0, 1,
     Ceiling[(Sin[(2*
            Pi/Prime[pn])*(n - (Prime[pn]^2 + 2*Prime[pn] - 5)/
             6)])^2]] == 1, 1, 0];

func3[n_] :=
  If[If[n - (Prime[pn]^2 + 4*Prime[pn] - 5)/6 < 0, 1,
     Ceiling[(Sin[(2*
            Pi/Prime[pn])*(n - (Prime[pn]^2 + 4*Prime[pn] - 5)/
             6)])^2]] == 1, 1, 0];

Clear[npp, npm];
n = nstart;
pnmax = IntegerPart[0.7835*nend^0.7656] + 5;
Print["====== The calculation results are shown below. ======"];
Print["nstart= ", nstart];
Print["nend= ", nend];
Print["---------"];

If[IntegerQ[nstart] && IntegerQ[nend] && nstart > 0 && nend > 0 && 
   nend > nstart && pnmax <= 999999999999,
  Do[
   If[Product[func2[n]*func3[n], {pn, 3, pnmax}] == 1, npm = n, 
    npm = 0];
   If[Product[func1[n], {pn, 3, pnmax}] == 1, npp = n, npp = 0];

   If[npm > 0, Print["npm= ", npm]];
   If[npm > 0, Print["(6n-1)+6 type prime= ", 6*npm + 5]];
   If[npm > 0, Print["PrimeQ[", 6*npm + 5, "]-> ", PrimeQ[6*npm + 5]]];
   If[npp > 0, Print["npp= ", npp]];
   If[npp > 0, Print["(6n+1)+6 type prime= ", 6*npp + 7]];
   If[npp > 0, Print["PrimeQ[", 6*npp + 7, "]-> ", PrimeQ[6*npp + 7]]];

   If[n == nend, Break[]], {n, nstart, nend}], 
  Print["===! The conditions are not met.==="]];

This is an example of ${\rm nstart} = 1$ and ${\rm nend} = 20$. The result of the calculation is output as follows:

====== The calculation results are shown below. ======
nstart= 1
nend= 20
---------

npm= 1
(6n-1)+6 type prime= 11
PrimeQ[11]-> True

npp= 1
(6n+1)+6 type prime= 13
PrimeQ[13]-> True

npm= 2
(6n-1)+6 type prime= 17
PrimeQ[17]-> True

npp= 2
(6n+1)+6 type prime= 19
PrimeQ[19]-> True

npm= 3
(6n-1)+6 type prime= 23
PrimeQ[23]-> True

npm= 4
(6n-1)+6 type prime= 29
PrimeQ[29]-> True

npp= 4
(6n+1)+6 type prime= 31
PrimeQ[31]-> True

npp= 5
(6n+1)+6 type prime= 37
PrimeQ[37]-> True

npm= 6
(6n-1)+6 type prime= 41
PrimeQ[41]-> True

npp= 6
(6n+1)+6 type prime= 43
PrimeQ[43]-> True

npm= 7
(6n-1)+6 type prime= 47
PrimeQ[47]-> True

npm= 8
(6n-1)+6 type prime= 53
PrimeQ[53]-> True

npm= 9
(6n-1)+6 type prime= 59
PrimeQ[59]-> True

npp= 9
(6n+1)+6 type prime= 61
PrimeQ[61]-> True

npp= 10
(6n+1)+6 type prime= 67
PrimeQ[67]-> True

npm= 11
(6n-1)+6 type prime= 71
PrimeQ[71]-> True

npp= 11
(6n+1)+6 type prime= 73
PrimeQ[73]-> True

npp= 12
(6n+1)+6 type prime= 79
PrimeQ[79]-> True

npm= 13
(6n-1)+6 type prime= 83
PrimeQ[83]-> True

npm= 14
(6n-1)+6 type prime= 89
PrimeQ[89]-> True

npp= 15
(6n+1)+6 type prime= 97
PrimeQ[97]-> True

npm= 16
(6n-1)+6 type prime= 101
PrimeQ[101]-> True

npp= 16
(6n+1)+6 type prime= 103
PrimeQ[103]-> True

npm= 17
(6n-1)+6 type prime= 107
PrimeQ[107]-> True

npp= 17
(6n+1)+6 type prime= 109
PrimeQ[109]-> True

npm= 18
(6n-1)+6 type prime= 113
PrimeQ[113]-> True

npp= 20
(6n+1)+6 type prime= 127
PrimeQ[127]-> True

First ${\rm nstart}$ and ${\rm nend}$ are displayed. Subsequently, the selected $np _m$ or $np _p$ is displayed and the corresponding prime number is displayed. In addition, the result of prime number judgment is shown.

Try running on a slightly larger number. In the example, ${\rm nstart} = 2000000000$ and ${\rm nend} = 2000000200$. The results are shown in Table-1. It took quite a while to calculate.

. $$ {\rm Table}\,1\;\;{\rm Example\,of\,prime \,numbers \,search \,using \,sine \,function}\\ ?{\rm nstart}=2000000000,\,{\rm nend}=2000000200?$$

\begin{array}{|c|c|c|}\hline npm,npp& (6n-1){\rm \;type \;prime}& (6n+1) \;{\rm type\;prime}\\ \hline 2000000011 &---&12000000073 \\ 2000000014 &---&12000000091 \\ 2000000022 &---&12000000139 \\ 2000000023 &12000000143&---\\ 2000000027 &---&12000000169\\ 2000000048 &12000000293&--- \\ 2000000053 &12000000323&--- \\ 2000000057 &12000000347&--- \\ 2000000059 &12000000359&---\\ 2000000061 &12000000371&--- \\ 2000000066 &12000000401&--- \\ 2000000067 &12000000407&--- \\ 2000000069 &---&12000000421 \\ 2000000071 &12000000431&--- \\ 2000000072 &12000000437&--- \\ 2000000079 &12000000479&--- \\ 2000000089 &---&12000000541 \\ 2000000090 &---&12000000547 \\ 2000000095 &---&12000000577 \\ 2000000118 &12000000713&--- \\ 2000000121 &12000000731&--- \\ 2000000123 &12000000743&--- \\ 2000000125 &---&12000000757 \\ 2000000127 &12000000767&--- \\ 2000000129 &---&12000000781 \\ 2000000130 &---&12000000787 \\ 2000000136 &12000000821&--- \\ 2000000140 &---&12000000847 \\ 2000000143 &12000000863&--- \\ 2000000151 &12000000911&--- \\ 2000000153 &12000000923&--- \\ 2000000156 &12000000941&--- \\ 2000000157 &---&12000000949 \\ 2000000163 &12000000983&--- \\ 2000000173 &12000001043&--- \\ 2000000174 &12000001049&12000001051 \\ 2000000187 &--- &12000001129 \\ 2000000191 &12000001151&--- \\ 2000000192 &--- &12000001159 \\ \hline \end{array}

(I couldn't write $np_m$ and $np_p$ on the table, so I made $npm$ and $npp$.)