Alas, the use of NVIDIA GPU leaves out many Mac users, including this user of a current iMac.

Can the GPU-specific code be rewritten so as to use Radeon GPUs?

These are great examples of the diverse uses of the Neural Networks framework. Is it possible to access MXNet's automatic differentiation (autograd) facility from within Mathematica? Automatic differentiation (distinct from Mathematica's symbolic differentiation capabilities) is a foundational technology for much of Machine Learning these days and it would be great if this could be done from within Mathematica. In my opinion, this could be really transformative.

Very nice! I like non-NN uses of the neural network functions :)

I made a simplified version of this concept:

Set some constants regarding the number of iterations, the frame bounds, and the resolution:

dims = {1000, 1000};
bounds = {{-2, 1}, {-1.5, 1.5}};
iterations = 200;

Create a network that runs one iteration:

stepnet=NetGraph[
    <|
        "re"->PartLayer[1],
        "im"->PartLayer[2],
        "sqre"->ThreadingLayer[#1^2-#2^2&],
        "sqim"->ThreadingLayer[2*#1*#2&],
        "catenate"->CatenateLayer[],
        "reshape"->ReshapeLayer[Prepend[dims,2]],
        "c"->ConstantPlusLayer["Biases"->{
            ConstantArray[N@Range[dims[[2]]]/dims[[2]]*(bounds[[1,2]]-bounds[[1,1]])+bounds[[1,1]],dims[[1]]],
            Transpose@ConstantArray[N@Range[dims[[1]]]/dims[[1]]*(bounds[[2,2]]-bounds[[2,1]])+bounds[[2,1]],dims[[2]]]}],
        "clip"->ElementwiseLayer[Clip[#,{-10000,10000}]&]
    |>,{
        NetPort["Input"]->{"re","im"}->{"sqre","sqim"}->"catenate"->"reshape"->"c"->"clip"->NetPort["Output"]
    },"Input"->Prepend[dims,2]]

Then create a network that runs the single-step-network repeatedly and calculates the squared norm at each resulting point:

net=NetGraph[<|
        "init"->ConstantArrayLayer["Array"->ConstantArray[0,Prepend[dims,2]]],
        "steps"->NetNestOperator[stepnet,iterations],
        "re"->PartLayer[1],
        "im"->PartLayer[2],
        "normsq"->ThreadingLayer[#1^2+#2^2&]
    |>,
    {"init"->"steps"->{"re","im"}->"normsq"->NetPort["Output"]}
]

Finally, evaluate the network:

Image@UnitStep[2^2 - net[]]

Attachments:

mandelbrotNN.nb

Nice post! In my experience, many built-in fractal functions is not very efficient. Compare with custom compilation function maybe better. The fastest implementation should be using CUDALink or OpenCLLink.

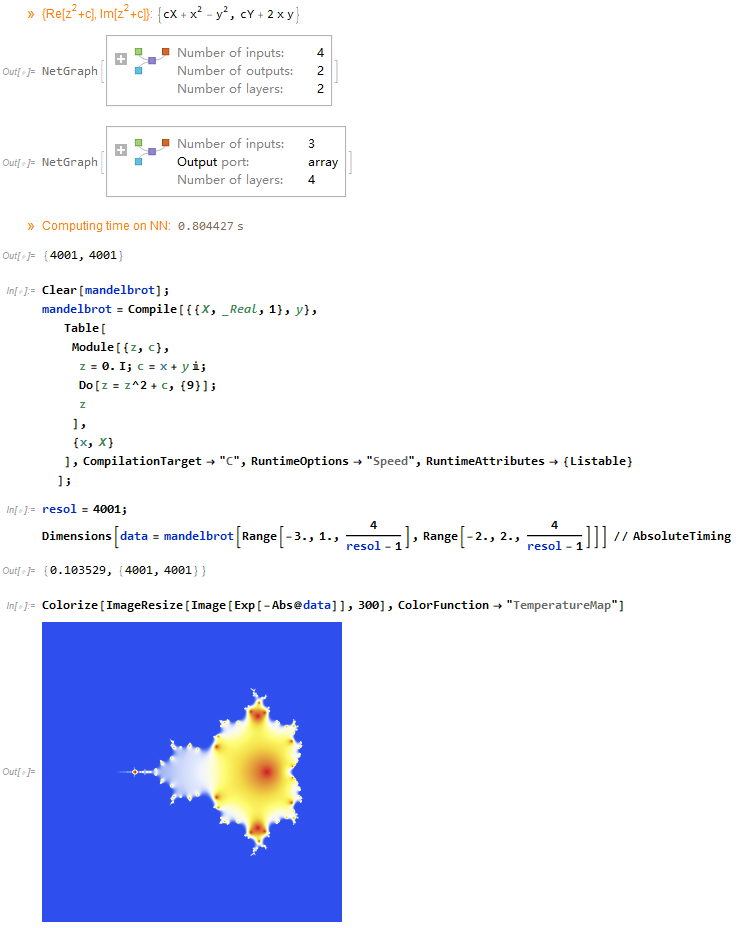
Clear[mandelbrot];
mandelbrot = Compile[{{X, _Real, 1}, y},
   Table[
    Module[{z, c},
     z = 0. I; c = x + y I;
     Do[z = z^2 + c, {9}];
     z
     ],
    {x, X}
    ], CompilationTarget -> "C", RuntimeOptions -> "Speed", 
   RuntimeAttributes -> {Listable}
   ];

resol = 4001;
Dimensions[data = mandelbrot[Range[-3., 1., 4/(resol - 1)],  Range[-2., 2., 4/(resol - 1)]]] // AbsoluteTiming
Colorize[ImageResize[Image[Exp[-Abs@data]], 300], ColorFunction -> "TemperatureMap"]

Another implementation, In my PC, it's about 10 times faster than the built-in.

Clear[mandelbrot];
mandelbrot = Compile[{{X, _Real, 1}, y, maxIt},
   Table[
    Module[{i = 0, z, c},
     z = c = x + y I;
     While[i++ <= maxIt && Re[z]^2 + Im[z]^2 < 4, z = z^2 + c];
     i
     ],
    {x, X}],
   CompilationTarget -> "C", RuntimeOptions -> "Speed", RuntimeAttributes -> {Listable}
];

resol=4000;
iterNum=200;
region={-3-2I,1+2I};

{{x1, x2}, {y1, y2}} = N@{Re@region, Im@region};

AbsoluteTiming[
Echo@AbsoluteTiming[data=mandelbrot[Range[x1,x2,(x2-x1)/(resol-1)],Range[y1,y2,(y2-y1)/(resol-1)],iterNum];];
colorTable=With[{n=Max[data]},
Developer`ToPackedArray@Table[If[i<n,List@@ColorData["M10DefaultFractalGradient",(i-1)/n],N@{0,0,0}],{i,n}]];
Image[colorTable[[#]]&/@data,"Real"]
]

MandelbrotSetPlot[region, MaxIterations -> iterNum, ImageResolution -> resol] // AbsoluteTiming

Attachments:

mandelbrotSet perf.nb

- Congratulations! This post is now featured in our Staff Pick column as distinguished by a badge on your profile of a Featured Contributor! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!