Group Abstract Group Abstract

Message Boards Message Boards

[GIF] :christmas_tree: (Conformal map of upper half-plane to triangle)

Conformal map of upper half-plane to triangle

:christmas_tree:

The Schwarz–Christoffel mappings are conformal transformations from the upper half-plane (or unit disk) to convex polygons; the existence of such maps is guaranteed by the Riemann Mapping Theorem. In general, these are somewhat challenging to compute/estimate, but in some cases they can be written down explicitly. For example, the following is an explicit Schwarz–Christoffel mapping to an equilateral triangle:

f[z_] := (E^((2 ? I)/3) Gamma[2/3])/(2^(1/3) Gamma[1/3] Gamma[4/3])
   (z - 1)^(1/3) Hypergeometric2F1[1/3, 2/3, 4/3, (1 - z)/2];

To make the animation, simply apply this map to the rectangular grid on the upper half-plane (and apply some cheats); the motion comes from sliding the vertical lines to the right.

Here's the code:

With[{r = 12., s = .67, cols = RGBColor /@ {"#f2f9f1", "#388e3c"}},
 Manipulate[
  Graphics[
   {cols[[1]],
    Polygon[{{s Cos[?/3] - 1, s Sin[?/3]}, {s Cos[2 ?/3], s Sin[?/3]}, {-1/2, Sqrt[3]/2}}],
    FaceForm[None], EdgeForm[Directive[cols[[1]], Thickness[.006]]],
    Polygon[{{0, 0}, {-1, 0}, {-1/2, Sqrt[3]/2}}],
    Thickness[.006], CapForm[None],
    Table[Line[Table[ReIm[f[t^3 + I y]], {t, -3., 3, 1/40}]], {y, 1, r}],
    Table[
     Line[Table[ReIm[f[x + I Exp[t]]], {t, -13., 4, 1/6}]],
     {x, -r + smootheststep[u], r + smootheststep[u], 1}]},
   ImageSize -> 540, Background -> cols[[2]],
   PlotRange -> {{-(6/5), 1/5}, {Sqrt[3]/4 - 7/10, Sqrt[3]/4 + 7/10}}],
  {u, 0, 1}]
 ]
POSTED BY: Clayton Shonkwiler
4 Replies
Sort By:
yuema.bit
yuema.bit
Posted 6 years ago

@Clayton, I just wondered that it seems that the function smootheststep[ ] is not the embedded in Mathematica, and I lost all the lines when I copy your code in my notebook.
POSTED BY: yuema.bit
J. M.
J. M.
Posted 6 years ago

Yes, Clayton forgot to include the definition for that function:

smootheststep[t_] := -20 t^7 + 70 t^6 - 84 t^5 + 35 t^4

Alternatively, you could also try using ResourceFunction["SmootherStep"] from the Function Repository, or any of a number of other sigmoidal functions like

ssteprat = #^3/(1 - 3 # (1 - #)) &;
POSTED BY: J. M.

enter image description here - Congratulations! This post is now featured in our Staff Pick column as distinguished by a badge on your profile of a Featured Contributor! Thank you, keep it coming, and consider contributing your work to the The Notebook Archive!

POSTED BY: EDITORIAL BOARD

A very neat idea, @Clayton, have not seen that yet around. Sooo it is that time of the year again when we get showered in code- and math- Xmas trees, awesome! I will post here a few the WL code for which I wrote the past. The first one comes from a very simple formula:

$$t * sin (t) ? Christmas Tree$$

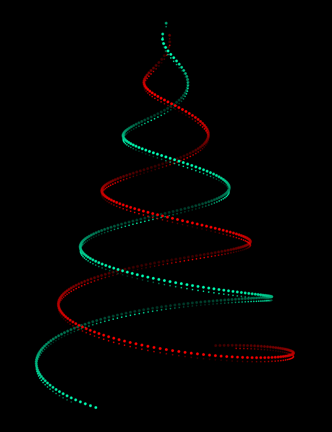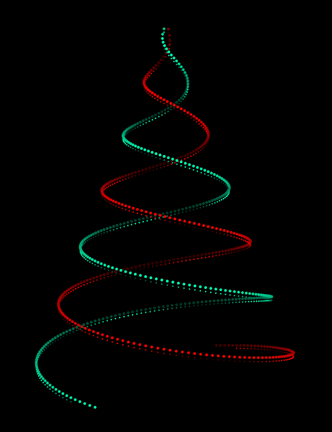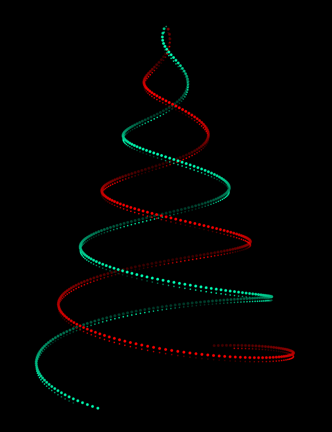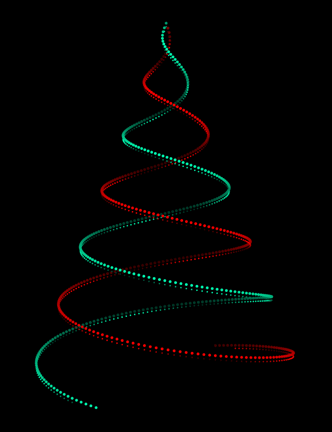
enter image description here

It is a simple expanding 3D spiral and it is made with the following code:

PD = .5; s[t_, f_] := t^.6 - f;
 dt[cl_, ps_, sg_, hf_, dp_, f_] := 
    {PointSize[ps], Hue[cl, 1, .6 + sg .4 Sin[hf s[t, f]]], 
     Point[{-sg s[t, f] Sin[s[t, f]], -sg s[t, f] Cos[s[t, f]], dp + s[t, f]}]};

 frames = ParallelTable[

    Graphics3D[Table[{dt[1, .01, -1, 1, 0, f], dt[.45, .01, 1, 1, 0, f], 
                      dt[1, .005, -1, 4, .2, f], dt[.45, .005, 1, 4, .2, f]}, 
 {t, 0, 200, PD}],

     ViewPoint -> Left, BoxRatios -> {1, 1, 1.3}, ViewVertical -> {0, 0, -1}, 
    ViewCenter -> {{0.5, 0.5, 0.5}, {0.5, 0.55}}, Boxed -> False, Lighting -> "Neutral", 
    PlotRange -> {{-20, 20}, {-20, 20}, {0, 20}}, Background -> Black],

   {f, 0, 1, .01}];

Export["tree.gif", frames]

Another one is made as ASCII art, which I really enjoy. Watch closely - the tree is also changing - snow sticks to branches then falls ;-)

enter image description here

To build it we start from simple observation that a bit of randomness builds a nice tree:

Column[Table[Row[RandomChoice[{"+", ".", "*", "~", "^", "o"}, k]], {k, 1, 35, 2}], Alignment -> Center]

enter image description here

And now with a bit more sophistication a scalable dynamic ASCII tree:

DynamicModule[{atoms, tree, pos, snow, p = .8, sz = 15},

 atoms = {
   Style["+", White],
   Style["*", White],
   Style["o", White],
   Style[".", Green],
   Style["~", Green],
   Style["^", Green],
   Style["^", Green]
   };

 pos = Flatten[Table[{m, n}, {m, 18}, {n, 2 m - 1}], 1];

 tree = Table[RandomChoice[atoms, k], {k, 1, 35, 2}];

 snow = Table[
   RotateLeft[ArrayPad[{RandomChoice[atoms[[1 ;; 2]]]}, {0, sz}, " "],
     RandomInteger[sz]], {sz + 1}];

 Dynamic[Refresh[

   Overlay[{

     tree[[Sequence @@ RandomChoice[pos]]] = RandomChoice[atoms];
     Column[Row /@ tree, Alignment -> Center, Background -> Black],

     Grid[
      snow = 
       RotateRight[
        RotateLeft[#, 
           RandomChoice[{(1 - p)/2, p, (1 - p)/2} -> {-1, 0, 1}]] & /@
          snow
        , {1, 0}]]

     }, Alignment -> Center]

   , UpdateInterval -> 0, TrackedSymbols -> {}]
  ]
 ]

And the last one is not mine, but just to make you smile, from xkcd:

enter image description here
POSTED BY: Vitaliy Kaurov
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard