When $n$ is a positive integer and both ( $6n-1$) and ( $6n+1$) are prime numbers, they are twin prime numbers. ( $6n-1$) is an infinite sequence of { $5,11,17,23, ?$}, and ( $6n+1$) is an infinite sequence of { $7,13,19,25, ?$}. An integer belonging to the sequence ( $6n-1$) is denoted as $n_m$, and an integer belonging to ( $6n+1$) is denoted as $n_p$. However, during the discussion, all positive integers are included in $n_m$ and $n_p$. Integers that do not belong to ( $6n?1$) are removed inside the program. Twin prime numbers have a relationship of $n_p=n_m+2$.
Equation ( $1$) determines whether $n_m$ and $n_p$ are twin primes or not. Give $n_m$ and $n_p$ to the right side of equation ( $1$), and give an arbitrary integer $s$. If $m$ has any integer solution, $n_m$ and $n_p$ are not twin primes. If there is no integer solution for $m$ , $n_m$ and $n_p$ are twin primes.
$$\begin{eqnarray} m_1&=&\frac{n_m-5+36s_1-36s_1^2}{6\cdot(6s_1-1)}\tag{1a} \\ m_2&=&\frac{n_m+1-36s_2^2}{6\cdot(6s_2+1)}\tag{1b} \\ m_3&=&\frac{n_p-7+48s_3-36s_3^2}{6\cdot(6s_3-1)}\tag{1c}\\ m_4&=&\frac{n_p+5+24s_4-36s_4^2}{6\cdot(6s_4+1)}\tag{1d} \end{eqnarray}$$
$$\begin{align*} & s=1,2,3\cdots \\ & n_m=(6n-1) \\ & n_p=(6n+1)=n_m+2 \\ & n=1,2,3\cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \end{align*} $$
$$\begin{equation} m= \left \{ \begin{array}{l} {\text {If there is at least one integer solution : }}n_m{\text { and }}n_p{\text { is not twin prime}} \; \\ {\text {If there is no integer solution : }}n_m{\text { and }}n_p{\text { is a twin prime number}} \end{array} \right.\\ \end{equation} $$
$s$ starts searching from $s=1$ and must search in step $1$ up to $s_{max}$. $s_{max}$ is determined depending on $n_p$. Equation ( $2$) was used to calculate $s_{max}$.
$$\begin{eqnarray} s_{max}=\frac{\sqrt{n_p}}{6}+1\tag{2}\\ \end{eqnarray}$$
$$\begin{align*} &s_{max} :{\text {Starting from }s=1{\text {, the upper limit of the search range (integer value) }}} \\ &n_p \text{ : Positive integer that tests twin primes = (6$n$ + 1) = (6$n$-1)+2}\\ \end{align*} $$
Note that $n_m$ and $n_p$ are given as arbitrary integers, and only those belonging to ( $6n?1$) in the program are selected.
The program is shown below.
nmstart = 1;
nmend = 1000;
"**********************************************";
nm = nmstart;
np = nm + 2;
nf = (nm + 1)/6;
smax = IntegerPart[Sqrt[np]/6] + 1;
Clear[f1, f2, f3, m1, m2, m3, m4];
Print["====== The calculation results are shown below. ======"];
func1[s_] := (nm - 5 + 36*s - 36*s^2)/(-6 + 36*s);
func2[s_] := (nm + 1 - 36*s^2)/(6 + 36*s);
func3[s_] := (np - 7 + 48*s - 36*s^2)/(-6 + 36*s);
func4[s_] := (np + 5 + 24*s - 36*s^2)/(6 + 36*s);
If[IntegerQ[nm] && nm > 0 && nmend > nmstart,
Print["nmstart= ", nm, "\nnmend= ", nmend];
Print["----------------"];
Do[
np = nm + 2;
smax = IntegerPart[Sqrt[np]/6] + 1;
nf = (nm + 1)/6;
f1 = 0;
f2 = 0;
Do[If[IntegerQ[func1[s]] && func1[s] > 0, m1 = 1, m1 = 0];
If[IntegerQ[func2[s]] && func2[s] > 0, m2 = 1, m2 = 0];
If[IntegerQ[func3[s]] && func3[s] > 0, m3 = 1, m3 = 0];
If[IntegerQ[func4[s]] && func4[s] > 0, m4 = 1, m4 = 0];
f1 = f1 + m1 + m2;
f2 = f2 + m3 + m4;
f3 = If[IntegerQ[nf], 1, 0];
If[s == smax, Break[]], {s, 1, smax}];
If[f1 == 0 && f2 == 0 && f3 == 1,
Print["Twin prime.\n", nm " is a prime number of (6n-1) type \n",
np " is a prime number of (6n+1) type "]];
If[f1 == 0 && f2 == 0 && f3 == 1,
Print["PrimeQ[", nm, "]= ", PrimeQ[nm]];
Print["PrimeQ[", np, "]= ", PrimeQ[np], "\n"]];
If[nm == nmend, Break[]], {nm, nmstart, nmend}];
If[f1 == 0 && f2 == 0 && f3 == 1,
Print["Twin prime.\n", nm " is a prime number of (6n-1) type \n",
np " is a prime number of (6n+1) type"]];
If[f1 == 0 && f2 == 0 && f3 == 1,
Print["PrimeQ[", nm, "]= ", PrimeQ[nm]];
Print["PrimeQ[", np, "]= ", PrimeQ[np "\n"]]],
Print["!! The condition has not been met."]];
This is an example in which the input values are $n_m start=1$ and $n_m end=1000$. The calculation result is as follows.
====== The calculation results are shown below. ======
nmstart= 1
nmend= 1000
----------------
Twin prime.
5 is a prime number of (6n-1) type
7 is a prime number of (6n+1) type
PrimeQ[5]= True
PrimeQ[7]= True
Twin prime.
11 is a prime number of (6n-1) type
13 is a prime number of (6n+1) type
PrimeQ[11]= True
PrimeQ[13]= True
Twin prime.
17 is a prime number of (6n-1) type
19 is a prime number of (6n+1) type
PrimeQ[17]= True
PrimeQ[19]= True
Twin prime.
29 is a prime number of (6n-1) type
31 is a prime number of (6n+1) type
PrimeQ[29]= True
PrimeQ[31]= True
Twin prime.
41 is a prime number of (6n-1) type
43 is a prime number of (6n+1) type
PrimeQ[41]= True
PrimeQ[43]= True
Twin prime.
59 is a prime number of (6n-1) type
61 is a prime number of (6n+1) type
PrimeQ[59]= True
PrimeQ[61]= True
Twin prime.
71 is a prime number of (6n-1) type
73 is a prime number of (6n+1) type
PrimeQ[71]= True
PrimeQ[73]= True
Twin prime.
101 is a prime number of (6n-1) type
103 is a prime number of (6n+1) type
PrimeQ[101]= True
PrimeQ[103]= True
Twin prime.
107 is a prime number of (6n-1) type
109 is a prime number of (6n+1) type
PrimeQ[107]= True
PrimeQ[109]= True
Twin prime.
137 is a prime number of (6n-1) type
139 is a prime number of (6n+1) type
PrimeQ[137]= True
PrimeQ[139]= True
Twin prime.
149 is a prime number of (6n-1) type
151 is a prime number of (6n+1) type
PrimeQ[149]= True
PrimeQ[151]= True
Twin prime.
179 is a prime number of (6n-1) type
181 is a prime number of (6n+1) type
PrimeQ[179]= True
PrimeQ[181]= True
Twin prime.
191 is a prime number of (6n-1) type
193 is a prime number of (6n+1) type
PrimeQ[191]= True
PrimeQ[193]= True
Twin prime.
197 is a prime number of (6n-1) type
199 is a prime number of (6n+1) type
PrimeQ[197]= True
PrimeQ[199]= True
Twin prime.
227 is a prime number of (6n-1) type
229 is a prime number of (6n+1) type
PrimeQ[227]= True
PrimeQ[229]= True
Twin prime.
239 is a prime number of (6n-1) type
241 is a prime number of (6n+1) type
PrimeQ[239]= True
PrimeQ[241]= True
Twin prime.
269 is a prime number of (6n-1) type
271 is a prime number of (6n+1) type
PrimeQ[269]= True
PrimeQ[271]= True
Twin prime.
281 is a prime number of (6n-1) type
283 is a prime number of (6n+1) type
PrimeQ[281]= True
PrimeQ[283]= True
Twin prime.
311 is a prime number of (6n-1) type
313 is a prime number of (6n+1) type
PrimeQ[311]= True
PrimeQ[313]= True
Twin prime.
347 is a prime number of (6n-1) type
349 is a prime number of (6n+1) type
PrimeQ[347]= True
PrimeQ[349]= True
Twin prime.
419 is a prime number of (6n-1) type
421 is a prime number of (6n+1) type
PrimeQ[419]= True
PrimeQ[421]= True
Twin prime.
431 is a prime number of (6n-1) type
433 is a prime number of (6n+1) type
PrimeQ[431]= True
PrimeQ[433]= True
Twin prime.
461 is a prime number of (6n-1) type
463 is a prime number of (6n+1) type
PrimeQ[461]= True
PrimeQ[463]= True
Twin prime.
521 is a prime number of (6n-1) type
523 is a prime number of (6n+1) type
PrimeQ[521]= True
PrimeQ[523]= True
Twin prime.
569 is a prime number of (6n-1) type
571 is a prime number of (6n+1) type
PrimeQ[569]= True
PrimeQ[571]= True
Twin prime.
599 is a prime number of (6n-1) type
601 is a prime number of (6n+1) type
PrimeQ[599]= True
PrimeQ[601]= True
Twin prime.
617 is a prime number of (6n-1) type
619 is a prime number of (6n+1) type
PrimeQ[617]= True
PrimeQ[619]= True
Twin prime.
641 is a prime number of (6n-1) type
643 is a prime number of (6n+1) type
PrimeQ[641]= True
PrimeQ[643]= True
Twin prime.
659 is a prime number of (6n-1) type
661 is a prime number of (6n+1) type
PrimeQ[659]= True
PrimeQ[661]= True
Twin prime.
809 is a prime number of (6n-1) type
811 is a prime number of (6n+1) type
PrimeQ[809]= True
PrimeQ[811]= True
Twin prime.
821 is a prime number of (6n-1) type
823 is a prime number of (6n+1) type
PrimeQ[821]= True
PrimeQ[823]= True
Twin prime.
827 is a prime number of (6n-1) type
829 is a prime number of (6n+1) type
PrimeQ[827]= True
PrimeQ[829]= True
Twin prime.
857 is a prime number of (6n-1) type
859 is a prime number of (6n+1) type
PrimeQ[857]= True
PrimeQ[859]= True
Twin prime.
881 is a prime number of (6n-1) type
883 is a prime number of (6n+1) type
PrimeQ[881]= True
PrimeQ[883]= True
In the display of the calculation result, $n_m start$ and $n_m end$ are shown first. Subsequently, the selected twin prime numbers and their types are displayed. Confirm that it is a prime number with ${\rm PrimeQ}$ [].
There were $34$ pairs of twin primes in the section where $n_m$ was $1$ to $1000$. How many twin primes are there between $1001$ and$ 2000$? The following graph plots the number of twin primes included in the section width $1000$.
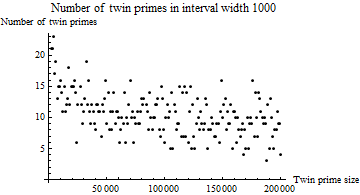
At the start, the twin prime numbers tend to decrease, but as the twin prime numbers increase, the decreasing trend appears to be slow.
$--------$
There are rules for twin primes greater than $5$.
? The end of $n_m$ is limited to [ $1,7,9$ ].
? The end of $n_p$ is limited to [ $3,9,1$ ].
This rule can be understood with a little thought. This rule can be used to eliminate unnecessary calculations, but it has not been applied this time.