Prime numbers greater than $5$ can be classified into ( $6n-1$) and ( $6n + 1$) types. All prime numbers greater than $5$ belong to either. The sequence ( $6n-1$) and the sequence ( $6n + 1$) include all prime numbers greater than $5$. At the same time, it also includes some composite numbers. The composite number included in the sequence ( $6n-1$) and the sequence ( $6n + 1$) can be specified by equation ( $1$).
All composite numbers included in the sequence ( $6n-1$) can be identified by equations ( $1{\rm a}$) and ( $1{\rm b}$). All composite numbers included in the sequence ( $6n + 1$) can be identified by equations ( $1{\rm c}$) and ( $1{\rm d}$). $n_m$ and $s$ are given to the right side of equations ( $1{\rm a}$) and ( $1{\rm b}$), and when there is no integer solution in $m$, $n_m$ is a prime of the ( $6n-1$) type. If $m$ has an integer solution, $n_m$ is a composite number. Similarly, when $n_p$ and $s$ are given to the right side of equations ( $1{\rm c}$) and ( $1{\rm d}$), and there is no integer solution in $m$, $n_p$ is a prime of the ( $6n + 1$) type. If there is an integer solution in $m$, $n_p$ is a composite number.
Equation ( $1$) selectively specifies only the composite numbers included in the sequences ( $6n-1$) and ( $6n + 1$). There is no indication of the number of composites not included in ( $6n-1$) and ( $6n + 1$).
$$\begin{eqnarray} m_1&=&\frac{n_m-5+36s_1-36s_1^2}{6\cdot(6s_1-1)}\tag{1a} \\ m_2&=&\frac{n_m+1-36s_2^2}{6\cdot(6s_2+1)}\tag{1b} \\ m_3&=&\frac{n_p-7+48s_3-36s_3^2}{6\cdot(6s_3-1)}\tag{1c}\\ m_4&=&\frac{n_p+5+24s_4-36s_4^2}{6\cdot(6s_4+1)}\tag{1d} \end{eqnarray}$$
$$\begin{align*} & s=1,2,3\cdots \\ & n_m=(6n-1) \\ & n_p=(6n+1)=n_m+2 \\ & n=1,2,3\cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \end{align*} $$
$$\begin{equation} m= \left \{ \begin{array}{l} {\text {If there is at least one integer solution : }}n_m{\text { and }}n_p{\text { is not prime}} \; \\ {\text {If there is no integer solution : }}n_m{\text { and }}n_p{\text { is a prime number}} \end{array} \right.\\ \end{equation} $$
$s$ starts searching from $s = 1$ and must search in step $1$ up to $s_{max}$. $s_{max}$ is determined depending on $n_p$. Equation ( $2$) was used to calculate $s_{max}$.
$$\begin{eqnarray} s_{max}=\frac{\sqrt{n_p}}{6}+1\tag{2}\\ \end{eqnarray}$$
$$\begin{align*} &s_{max} :{\text {Starting from }s=1{\text {, the upper limit of the search range (integer value) }}} \\ &n_p \text{ : Positive integer that tests twin primes = (6$n$ + 1) = (6$n$-1)+2}\\ \end{align*} $$
The program is shown below.
nmstart = 1;
nmend = 100;
"**********************************************";
nm = nmstart;
np = nm + 2;
mf = (nm + 1)/6;
pf = (np - 1)/6;
smax = IntegerPart[Sqrt[np]/6] + 1;
cm = 0;
cp = 0;
Clear[f1, f2, f3, m1, m2, m3, m4];
Print["====== The calculation results are shown below. ======"];
func1[s_] := (nm - 5 + 36*s - 36*s^2)/(-6 + 36*s);
func2[s_] := (nm + 1 - 36*s^2)/(6 + 36*s);
func3[s_] := (np - 7 + 48*s - 36*s^2)/(-6 + 36*s);
func4[s_] := (np + 5 + 24*s - 36*s^2)/(6 + 36*s);
If[IntegerQ[nm] && nm > 0 && nmend > nmstart,
Print["nmstart= ", nm, "\nnmend= ", nmend];
Print["----------------"];
Do[
np = nm + 2;
smax = IntegerPart[Sqrt[np]/6] + 1;
mf = (nm + 1)/6;
pf = (np - 1)/6;
f1 = 0;
f2 = 0;
Do[If[IntegerQ[func1[s]] && func1[s] > 0, m1 = 1, m1 = 0];
If[IntegerQ[func2[s]] && func2[s] > 0, m2 = 1, m2 = 0];
If[IntegerQ[func3[s]] && func3[s] > 0, m3 = 1, m3 = 0];
If[IntegerQ[func4[s]] && func4[s] > 0, m4 = 1, m4 = 0];
f1 = f1 + m1 + m2;
f2 = f2 + m3 + m4;
f3 = If[IntegerQ[mf], 1, 0];
f4 = If[IntegerQ[pf], 1, 0];
If[s == smax, Break[]], {s, 1, smax}];
If[f1 == 0 && f3 == 1,
Print[nm " is a prime number of (6n-1) type "]];
If[f1 == 0 && f3 == 1,
Print["PrimeQ[", nm, "]= ", PrimeQ[nm], "\n"]];
If[f2 == 0 && f4 == 1,
Print[np " is a prime number of (6n+1) type "]];
If[f2 == 0 && f4 == 1,
Print["PrimeQ[", np, "]= ", PrimeQ[np], "\n"]];
If[f1 == 0 && f3 == 1, cm = cm + 1, cm + 0];
If[f2 == 0 && f4 == 1, cp = cp + 1, cp + 0];
If[nm == nmend, Break[]], {nm, nmstart, nmend}];
If[f1 == 0 && f3 == 1,
Print[nm " is a prime number of (6n-1) type "]];
If[f1 == 0 && f3 == 1,
Print["PrimeQ[", nm, "]= ", PrimeQ[nm], "\n"]];
If[f1 == 0 && f3 == 1, cm = cm + 1, cm + 0];
If[f2 == 0 && f4 == 1, cp = cp + 1, cp + 0];
If[f2 == 0 && f4 == 1,
Print[np " is a prime number of (6n+1) type "]];
If[f2 == 0 && f4 == 1,
Print["PrimeQ[", np, "]= ", PrimeQ[np], "\n"]];
Print["------ Count at interval: ", nmstart, " to ", nmend "------"];
Print["Count (6n-1)type prime= ", cm];
Print["Count (6n+1)type prime= ", cp],
Print["!! The condition has not been met."]];
This is an example in which the input values are $n_m start = 1$ and $n_m end = 100$. The calculation result is as follows.
====== The calculation results are shown below. ======
nmstart= 1
nmend= 100
----------------
5 is a prime number of (6n-1) type
PrimeQ[5]= True
7 is a prime number of (6n+1) type
PrimeQ[7]= True
11 is a prime number of (6n-1) type
PrimeQ[11]= True
13 is a prime number of (6n+1) type
PrimeQ[13]= True
17 is a prime number of (6n-1) type
PrimeQ[17]= True
19 is a prime number of (6n+1) type
PrimeQ[19]= True
23 is a prime number of (6n-1) type
PrimeQ[23]= True
29 is a prime number of (6n-1) type
PrimeQ[29]= True
31 is a prime number of (6n+1) type
PrimeQ[31]= True
37 is a prime number of (6n+1) type
PrimeQ[37]= True
41 is a prime number of (6n-1) type
PrimeQ[41]= True
43 is a prime number of (6n+1) type
PrimeQ[43]= True
47 is a prime number of (6n-1) type
PrimeQ[47]= True
53 is a prime number of (6n-1) type
PrimeQ[53]= True
59 is a prime number of (6n-1) type
PrimeQ[59]= True
61 is a prime number of (6n+1) type
PrimeQ[61]= True
67 is a prime number of (6n+1) type
PrimeQ[67]= True
71 is a prime number of (6n-1) type
PrimeQ[71]= True
73 is a prime number of (6n+1) type
PrimeQ[73]= True
79 is a prime number of (6n+1) type
PrimeQ[79]= True
83 is a prime number of (6n-1) type
PrimeQ[83]= True
89 is a prime number of (6n-1) type
PrimeQ[89]= True
97 is a prime number of (6n+1) type
PrimeQ[97]= True
------ Count at interval: 1 to 100 ------
Count (6n-1)type prime= 12
Count (6n+1)type prime= 11
In the display of the calculation result, $n_m start$ and $n_m end$ are shown first. Subsequently, the selected prime number and its type are displayed. Furthermore, confirm that it is a prime number with ${\rm PrimeQ} []$. Finally, the number and type of prime numbers existing in the search section are displayed.
Fig. 1 shows the number of ( $6n-1$) type prime numbers and ( $6n + 1$) type prime numbers. The number $?$ ( $x$) of prime numbers existing below $x$ is divided into ( $6n-1$) type and ( $6n + 1$) type. The two appear almost overlapping, but not completely.
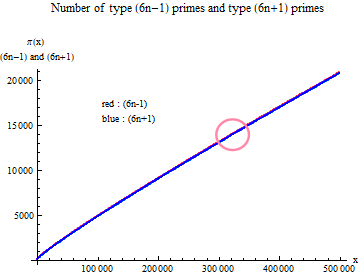
Fig. 1 Number of type ( $6n-1$) primes and type ( $6n+1$) primes
.
Fig. 2 is an enlarged view of the circular mark in Fig. 1. Looking at this section in an enlarged view, it can be seen that the prime number (red dot) of the ( $6n-1$) type is greater than the prime number (blue dot) of the ( $6n + 1$) type.
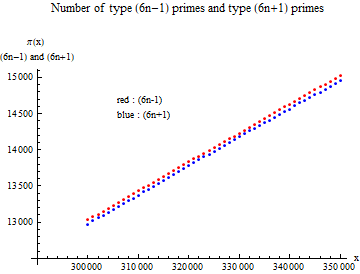
Fig. 2 Partial enlarged view
.
Next, the section width was set to $1000$, and the number of prime numbers included in each section was counted. It is plotted in Fig3.With a small prime number, the number of prime numbers included in the section is relatively large. When the prime number becomes large, the number of prime numbers generated in the section decreases. As the number increases, the rate of decrease decreases. Since the prime numbers have been proved to exist infinitely, it looks like a distribution curve consistent with it. The randomness of the ( $6n-1$) and ( $6n + 1$) types appears at the same level.
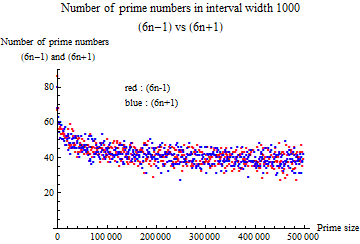
Fig. 3 Number of prime numbers in interval width $1000$
.
Within the range of data handled, the number of ( $6n-1$) type primes is larger than the number of ( $6n + 1$) type primes. It is not known whether this trend will continue indefinitely.
Looking at Fig4, one can imagine the periodicity behind the prime numbers from the analogy of the Fourier series that a sawtooth wave is created by superposition of sine functions. Equation ( $1$) is also a function having periodicity. Although Fig4 is based on data collected with a section width of $1000$, a similar tendency can be seen when the section width is reduced to $100$.
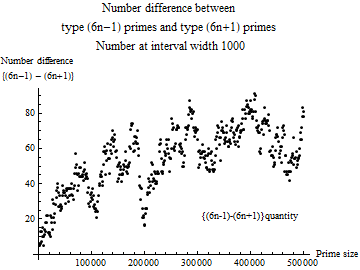
Fig. 4 Difference between the number of type ( $6n-1$) prime numbers and type ( $6n+1$) prime numbers (interval width $1000$)
.
Fig. 5 shows prime numbers of the ( $6n-1$) type and ( $6n + 1$) type in terms of incidence. One of the plot points represents the number of prime numbers in the section width of $1000$. If the number is the same between the ( $6n-1$) type and the ( $6n + 1$) type, the occurrence ratio is $1$, but it always exceeds $1$ in this data section. That is, many ( $6n-1$) -type prime numbers are generated. It is not known how long this trend will continue. Note that the X axis is drawn at Y = 1.
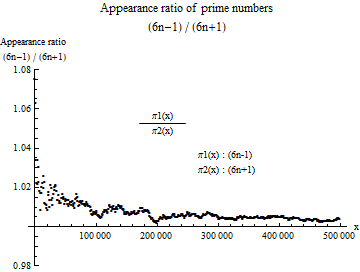
Fig. 5 Appearance ratio of prime numbers
.
$--------$
The five plots shown above are based on the number of prime numbers actually counted.
The same figure can be drawn theoretically from equation ( $1$).