MODERATOR NOTE: a submission to computations art contest, see more: https://wolfr.am/CompArt-22
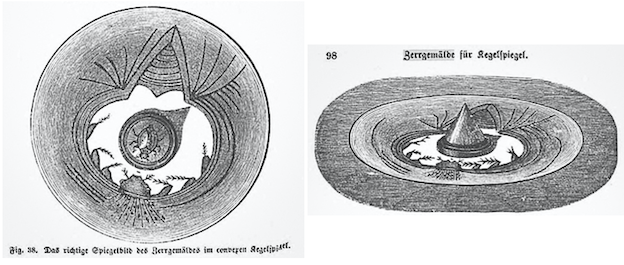
People have been trying to disguise "secret" images so they can only be seen by the use of a special device, like a mirror. Cylindrical- and conical mirrors have been very popular for revealing these "anamorphic" images. Witness is this example from the book "Licht und Farbe" by Franz Josef Pisko dating from back from 1876.
Mirror (or catoptric) anamorphism is the inverse of reflection: Whereas in reflection, one attempts to find out how a real image will look in a mirror, anamorphism explores how a reflection should look so it is displayed as realistic in a mirror. I made several Wolfram Demonstrations related to anamorphic transformations in the past. One in particular is about Conical Anamorphic Projection of Photographic Images.

Here is the function conicAnamorphMapCF used in these demonstrations. The function will take a point pt and transform it into its anamorphic map, using the law of reflection in a conical mirror with opening angle [Alpha] and a viewpoint at (0, 0, v) .
conicAnmorphMapCF =
Compile[{{pt, _Real, 1}, {\[Alpha], _Real}, {v, _Real}},
Module[{x, y, t}, {x, y} = pt;
t = Sqrt[
x^2 + y^2]; {x,
y} (t (v - Cot[\[Alpha]/2]) -
v (-1 + t) Cot[\[Alpha]/
2] Tan[\[Alpha] - ArcTan[t/v]])/(t (v -
t Cot[\[Alpha]/2]))], CompilationTarget -> "C",
Parallelization -> True, RuntimeAttributes -> {Listable},
RuntimeOptions -> "Speed"];
This GIF shows the function in action: an anamorphic point S, moving along the red curve is observed by the viewer at V as a reflected point P moving along the blue line in the base of the cone.
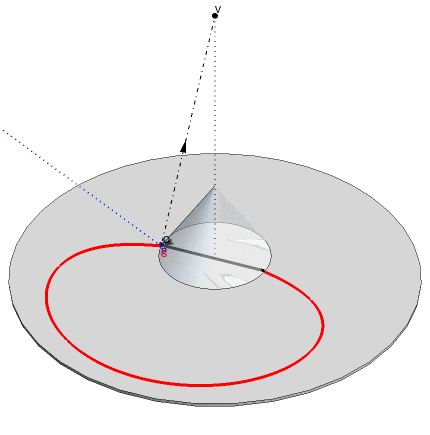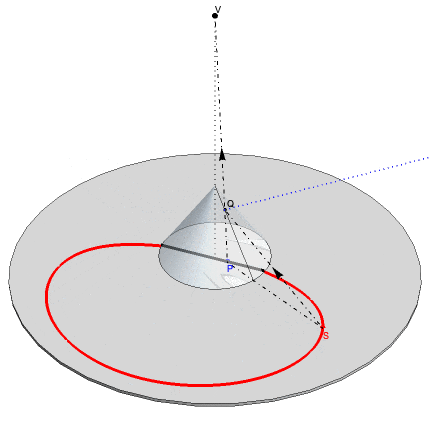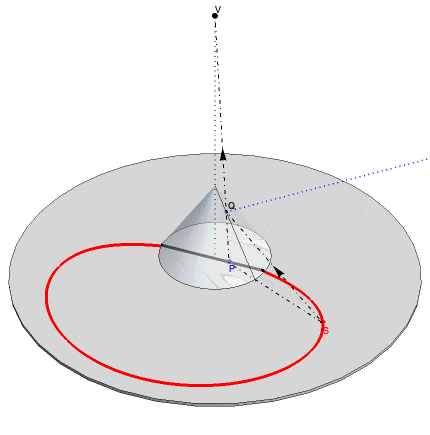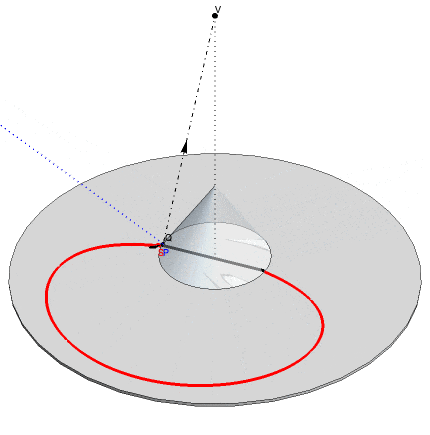
To make images ready for an anamorphic transformation, we partition them into polygonal sections. A classical raster- like division is OK, but for use in conical anamorphism, a radial partition into polygons is best. A radial division of the image consists of concentric polygons, centered around the midpoint of the image. The vertices of these quadrilaterals are the intersections of a set of concentric circles and another (perpendicular) set of radial lines departing from the center. The function imageRadialSplit will convert and image into such a set of radially oriented quadrilaterals:
imageRadialSplit[im_Image] :=
Module[{resoR, resoC, vertices, polyRule, polys, centroids,
radialData}, resoR = 1/2 First[ImageDimensions[im]];
resoC = 3 resoR;
vertices =
ParallelTable[
CirclePoints[{resoR, resoR}, i^2/resoR, resoC], {i, 1,
resoR + 1}]/resoR - 1;
polyRule = {{a : {_?NumericQ, _?NumericQ}, b_}, {c_, d_}} :>
Polygon[{a, b, d, c}];
polys = ParallelTable[
Partition[Transpose[vertices[[i ;; i + 1]]], 2, 1, {1, 1}], {i,
resoR - 1}] /. polyRule;
centroids = ParallelMap[RegionCentroid, polys, {2}];
radialData =
Transpose[ParallelMap[Flatten[#1, 1] &, {polys, centroids}]];
ParallelMap[{FaceForm[
RGBColor @@ ImageValue[im, #1[[2]] resoR + {resoR, resoR}]],
EdgeForm[], #1[[1]]} &, radialData]]
During the anamorphic transformation, the vertices of the quadrilaterals are mapped to new positions. These deformed quadrilaterals are given the colors of the centroids of the original polygons. Many circular images, such as logos, etc can be transformed that way and be observed as realistic looking down vertically in the apex of a conical mirror.
wolframLogo =
Import["https://upload.wikimedia.org/wikipedia/en/thumb/1/17/\
Wolfram_Language_Logo_2016.svg/1200px-Wolfram_Language_Logo_2016.svg.\
png"];
The following code generates a row of two 3D views of a conical mirror reflection of the Wolfram logo. The right picture is what an observer sees looking vertically down onto the apex of the mirror.
Module[{im, data2D, data3D, anaData},
im = ImageResize[ImageAdjust[wolframLogo], 300];
data2D = imageRadialSplit[im];
data3D = data2D /. {x_?NumericQ, y_} :> {x, y, .001};
anaData =
MapAt[conicAnmorphMapCF[#1, 72. \[Degree], 6] &,
data2D, {All, -1, All, All}] /. {x_?NumericQ, y_?NumericQ} :> {x,
y, .001};
GraphicsGrid[{(Graphics3D[{{Opacity[.5],
Cone[{{0, 0, 0}, {0, 0, 1.5}}, 1]}, {LightGray, Opacity[.75],
Cylinder[{{0, 0, 0}, {0, 0, .0005}}, 4.25]}, data3D,
anaData}, PlotRange -> {{-5, 5}, {-5, 5}, {0, 2}},
Boxed -> False,
Lighting -> {{"Ambient", GrayLevel[.5]}, {"Point",
White, {0, 25, 25}}}, ViewAngle -> 5 \[Degree],
ViewPoint -> #1, ImageSize -> 550] &) /@ {{0., -8.138481,
6.14}, {0, -.1, 10.14}}}, Spacings -> 0, ImageSize -> 600]]
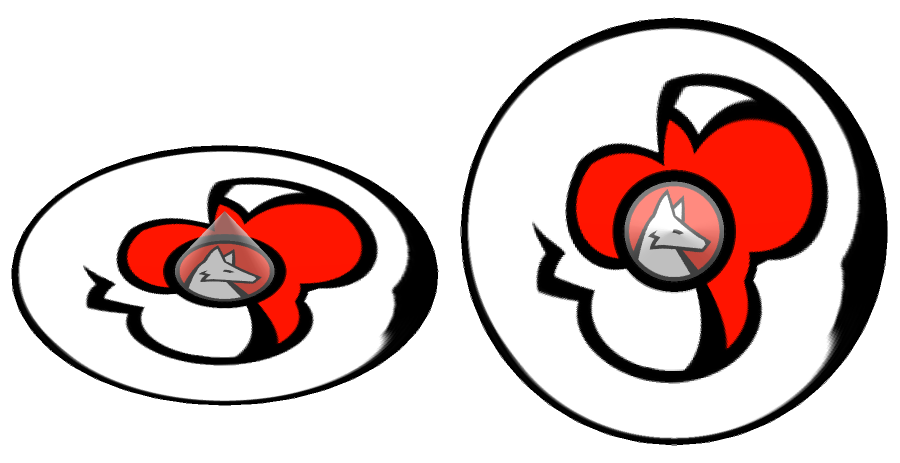
Here is a another one using a legacy coca cola logo:


Whereas a cylindrical mirror is very easy to make with e.g a coke can wrapped in reflective window film, a conical mirror is much harder to produce. Especially the area around the apex needs to be geometrically perfect since this will be the the most deformed and magnified. Where there is no image information around the apex, as here with the Amazon logo, this gives good results.

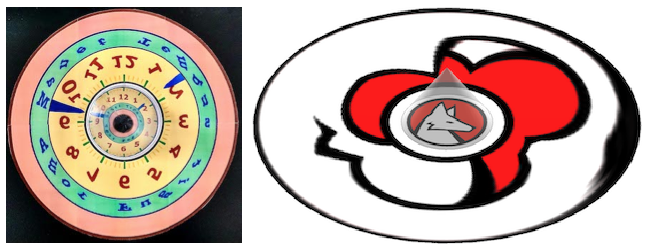
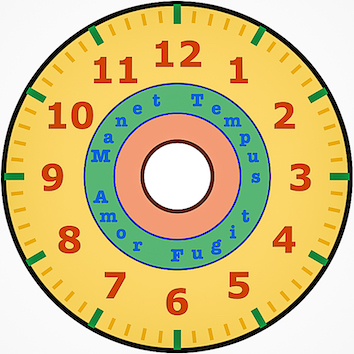
To avoid the "apex problem", I resorted to a frustum or truncated cone where the apex problem is avoided. A 3D printed cone with reflective film around, proved to be a sufficiently accurate solution for the image of a clock, where I could black out the center without losing much information.

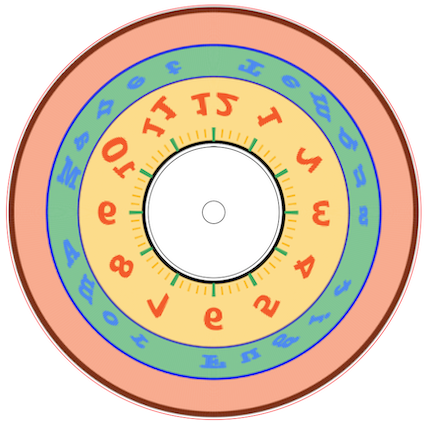
We first make a Graphics image of a clock dial.
Module[{}, txt = "Tempus tiguF romA Manet";
txtChars = Characters[txt];
cols = {RGBColor[0.965, 0.3285`, 0.0785],
RGBColor[0.266, 0.516, 0.958], RGBColor[0.207, 0.652, 0.324],
RGBColor[0.988, 0.73, 0.0195]};
clock = Image[
Graphics[{{AbsoluteThickness[8], Circle[], AbsoluteThickness[6],
Circle[{0, 0}, .2], Blue, AbsoluteThickness[3],
Circle[{0, 0}, .53], Circle[{0, 0}, .36], Opacity[.65],
cols[[3]], Annulus[{0, 0}, {.365, .525}], Opacity[.5],
cols[[4]], Annulus[{0, 0}, {.53, .99}], cols[[1]],
Annulus[{0, 0}, {.19, .355}]}, {Thickness[0.01], cols[[4]],
Table[Line[{0.9 {Cos[a], Sin[a]}, 0.95 {Cos[a], Sin[a]}}], {a,
0, 2 \[Pi], \[Pi]/30}]}, {Thickness[0.02], cols[[3]],
Table[Line[{0.9 {Cos[a], Sin[a]}, 0.975 {Cos[a], Sin[a]}}], {a,
0, 2 \[Pi], \[Pi]/6}]},
Style[Table[
Text[i, 0.71 {Cos[1/6 (-i) \[Pi] + \[Pi]/2],
Sin[1/6 (-i) \[Pi] + \[Pi]/2]}], {i, 1, 12}], "Label", Bold,
cols[[1]], 55],
Style[Table[
Text[txtChars[[i]],
0.45 {Cos[1/12 (-i) \[Pi] + \[Pi]/2],
Sin[1/12 (-i) \[Pi] + \[Pi]/2]}], {i, 1, 23}], "Label",
Bold, cols[[2]], FontFamily -> "American Typewriter", 28]}]]]
This shows the clock image entered into the code used for the Wolfram logo above:
Module[{im, data2D, data3D, anaData}, im = ImageResize[clock, 300];
data2D = imageRadialSplit[im];
data3D = data2D /. {x_?NumericQ, y_} :> {x, y, .001};
anaData =
MapAt[conicAnmorphMapCF[#1, 72. \[Degree], 6] &,
data2D, {All, -1, All, All}] /. {x_?NumericQ, y_?NumericQ} :> {x,
y, .001};
GraphicsGrid[{(Graphics3D[{{Opacity[.5],
Cone[{{0, 0, 0}, {0, 0, 1.5}}, 1]}, {LightGray, Opacity[.75],
Cylinder[{{0, 0, 0}, {0, 0, .0005}}, 4.25]}, data3D,
anaData}, PlotRange -> {{-5, 5}, {-5, 5}, {0, 2}},
Boxed -> False,
Lighting -> {{"Ambient", GrayLevel[.5]}, {"Point",
White, {0, 25, 25}}}, ViewAngle -> 5 \[Degree],
ViewPoint -> #1, ImageSize -> 550] &) /@ {{0., -8.138481,
6.14}, {0, -.1, 10.14}}}, Spacings -> 0, ImageSize -> 600]]
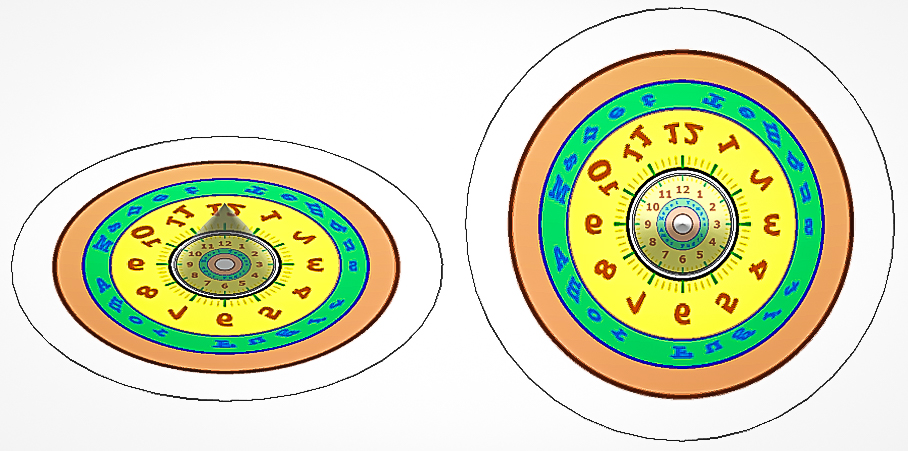
This makes a printout for the anamorphic clock dial:
Module[{pic = clock, im, \[Alpha] = 70 \[Degree], pixelPolys,
anaPixelPolys},
im = ImageResize[ImageAdjust[ColorConvert[pic, "RGB"]], 500];
pixelPolys = imageRadialSplitX[im, 1];
anaPixelPolys =
MapAt[conicAnamorphMapVCF[#1, \[Alpha], 4] &,
pixelPolys, {All, -1, All, All}];
anaClock =
Graphics[{If[True, pixelPolys, Nothing],
anaPixelPolys, {Circle[], Circle[{0, 0}, .172]}},
PlotRange -> 1.05 anaradius]]
We put our reflective frustum on top:

This is what you see looking straight down the mirror on our "anamorphic clock"!
