Hi. I calculated the intensity of light in double-slit experiment assuming the wave of light is the sine wave and plotted it in Mathematica.
Manipulate[
{Graphics[
{{RGBColor[0, 0.42, 0.65],
Line[{{0, -3 10^-6}, {0, 3 10^-6}}]}, {RGBColor[0, 0.42, 0.65],
Line[{{L, -3 10^-6}, {L, 3 10^-6}}]}, {Point[{0, 0.5 d}],
PointSize[10^-7]},
Text["Slit1", {-0.2, 0.5 d + 0.2 10^-6}], {Point[{0, -0.5 d}],
PointSize[Large]}, Text["Slit2", {-0.22, -0.5 d - 0.2 10^-6}],
Point[{0, -0.5 d}], Text["Screen", {L + 0.3, 2.8 10^-6}],
Point[{L, 0}], Text["Origin", {L + 0.35, -0.2 10^-6}],
Line[{{0, -0.5 d}, {L, x}}], Line[{{0, 0.5 d}, {L, x}}],
Arrow[{{L + 0.1, 0}, {L + 0.1, x}}], {Thin,
Arrow[{{-0.1, -0.5 d}, {-0.1, 0.5 d}}]}, {Thin,
Arrow[{{-0.1, 0.5 d}, {-0.1, -0.5 d}}]}, {Thin,
Arrow[{{0, -2.9 10^-6}, {L, -2.9 10^-6}}]}, {Thin,
Arrow[{{L, -2.9 10^-6}, {0, -2.9 10^-6}}]},
Text["x", {L + 0.25, 0.5 x}], Text["d", {-0.25, 0}],
Text["L", {0.5 L, -2.8 10^-6}]},
AspectRatio -> 1,
PlotRange -> {{-0.6, 4}, {-3.5 10^-6, 3.1 10^-6}},
PlotLabel -> "Diagram of the Experiment ",
ImageSize -> Medium],
Plot[1/(L^2 + (x - 0.5 d)^2) + 1/(L^2 + (x + 0.5 d)^2) + (
2 Cos[2 Pi Abs[
Sqrt[L^2 + (x - 0.5 d)^2] -
Sqrt[L^2 + (x + 0.5 d)^2]]/\[Lambda]])/(
Sqrt[L^2 + (x - 0.5 d)^2] Sqrt[L^2 + (x + 0.5 d)^2]), {x, -8, 8},
PlotLabel -> "Intensity of Light in Double Slit Experiment",
AxesLabel -> {"x", "Intensity"},
PlotRange -> {{-8.1, 8.1}, {-0.1, 4.1}}, ImageSize -> Large]}
, {L, 1, 3}, {d, 10^-6, 3 10^-6}, {\[Lambda], 3 10^-7,
8 10^-7}, {x, -2.7 10^-6, 2.7 10^-6}]
And I also tried to get an image of the screen in the experiment using DensityPlot function. However, As I make an input and operate it, it always shows such a strange image.
Manipulate[
DensityPlot[
1/(L^2 + (x - 0.5 d)^2) + 1/(L^2 + (x + 0.5 d)^2) + (
2 Cos[2 Pi Abs[
Sqrt[L^2 + (x - 0.5 d)^2] -
Sqrt[L^2 + (x + 0.5 d)^2]]/\[Lambda]])/(
Sqrt[L^2 + (x - 0.5 d)^2] Sqrt[L^2 + (x + 0.5 d)^2]), {x, -8,
8}, {y, 0, 1}, ColorFunctionScaling -> False,
ColorFunction -> GrayLevel, AspectRatio -> 0.125,
PlotLegends -> Automatic, ImageSize -> Full], {L, 1, 3}, {d, 10^-6,
3 10^-6}, {\[Lambda], 3 10^-7, 8 10^-7}]
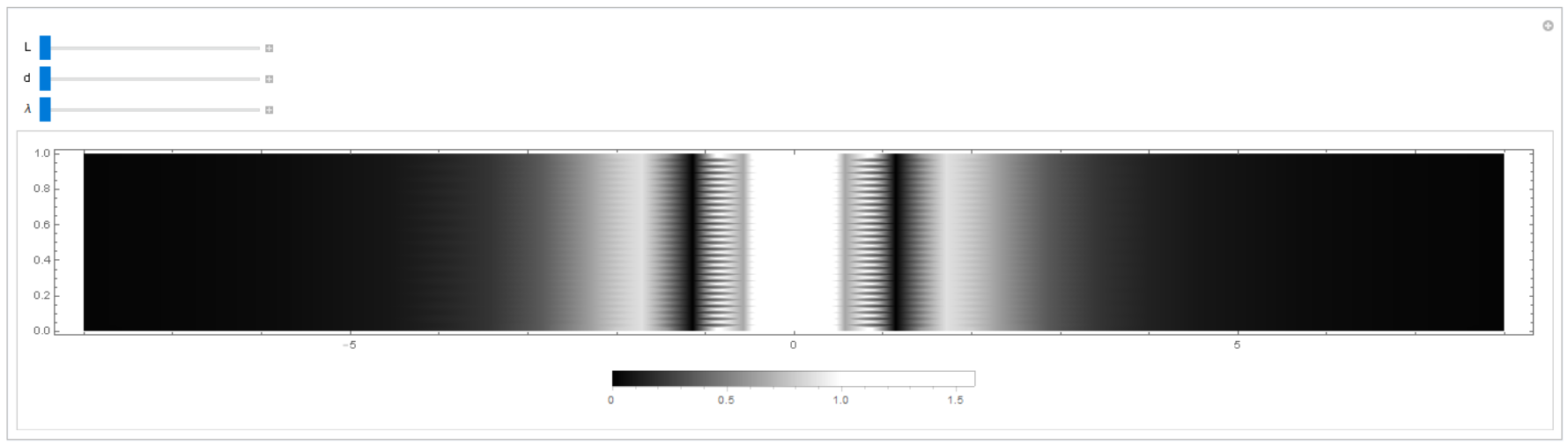
Though I didn't include 'y value' in the expression, there are some horizontal lines in the output image. Could you explain what just happened?