Yes, it can be done like this:
(In that case, I maximize the "CCtest")
corrN[t1_, t2_, n_] :=
Module[{train, lm, test, cx, gg, YPtrain, Ytrain, CCtrain, YPtest,
Ytest, CCtest, x},
MaximalBy[
Table[train = SortBy[RandomSample[data, t1], First];
lm = LinearModelFit[train, x, x];
cx = CoefficientList[Normal@lm, x];
gg[x_, y_] := (cx[[1]] + cx[[2]]*x);
YPtrain = Map[gg[#[[1]], #[[2]]] &, train];
Ytrain = train[[All, 2]]; CCtrain = Correlation[YPtrain, Ytrain];
test = SortBy[RandomSample[train, t2], First];
YPtest = Map[gg[#[[1]], #[[2]]] &, test]; Ytest = test[[All, 2]];
CCtest =
Correlation[YPtest, Ytest]; {Style[CCtest, Red] ->
Style["CCtest", Red],
Style[CCtrain, Blue] -> Style["CCtrain", Blue], {"YPtrain",
YPtrain}, {"Ytrain", Ytrain}, {"YPtest", YPtest}, {"YTest",
Ytest}, {Style[ToString[cx[[1]] + cx[[2]]*"x"], Purple]},
ListLinePlot[{YPtrain, Ytrain},
PlotLegends -> {"YPTrain", "Ytrain"}, ImageSize -> Medium],
ListLinePlot[{YPtest, Ytest}, PlotLegends -> {"YPtest", "Ytest"},
ImageSize -> Medium]}, n], First]]
With n=20:
corrN[12, 4, 20]
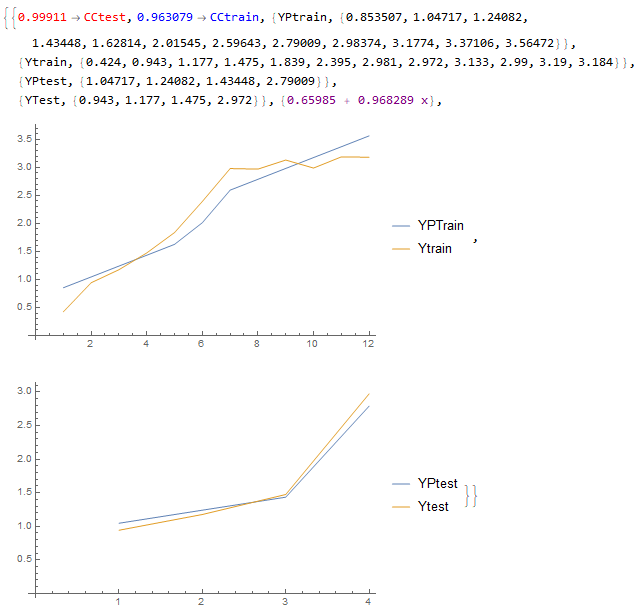
And below, a way to maximize "CCtrain" and "CCtest" at the same time:
corrAll[t1_, t2_, n_] :=
Module[{ff, train, lm, test, cx, gg, YPtrain, Ytrain, CCtrain,
YPtest, Ytest, CCtest, x, vc},
vc = Table[train = SortBy[RandomSample[data, t1], First];
lm = LinearModelFit[train, x, x];
cx = CoefficientList[Normal@lm, x];
gg[x_, y_] := (cx[[1]] + cx[[2]]*x);
YPtrain = Map[gg[#[[1]], #[[2]]] &, train];
Ytrain = train[[All, 2]]; CCtrain = Correlation[YPtrain, Ytrain];
test = SortBy[RandomSample[train, t2], First];
YPtest = Map[gg[#[[1]], #[[2]]] &, test]; Ytest = test[[All, 2]];
CCtest = Correlation[YPtest, Ytest];
ff = {CCtest,
CCtrain, {"YPtrain", YPtrain}, {"Ytrain", Ytrain}, {"YPtest",
YPtest}, {"YTest",
Ytest}, {Style[ToString[cx[[1]] + cx[[2]]*"x"], Purple]},
ListLinePlot[{YPtrain, Ytrain},
PlotLegends -> {"YPTrain", "Ytrain"}, ImageSize -> Medium],
ListLinePlot[{YPtest, Ytest},
PlotLegends -> {"YPtest", "Ytest"}, ImageSize -> Medium]}; {ff,
ff[[1]]*ff[[2]]}, n];
vc[[Position[vc, MaximalBy[vc, Last][[1]]][[1, 1]], 1]]]
With n=100:
corrAll[12, 4, 100]
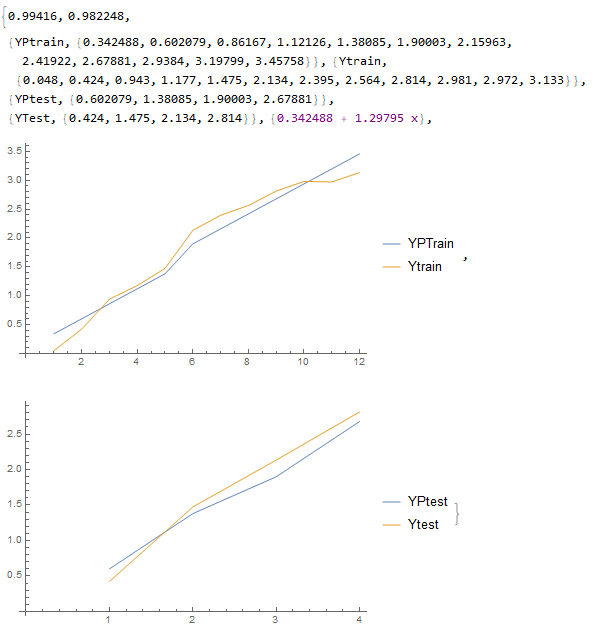
..