Yes, rules are not functions, that is, they are not necessarily deterministic. I'm not sure which papers you are referring to, but, maybe, the docs on event ordering and selection could be helpful.

This sketch helped me make sense of it:

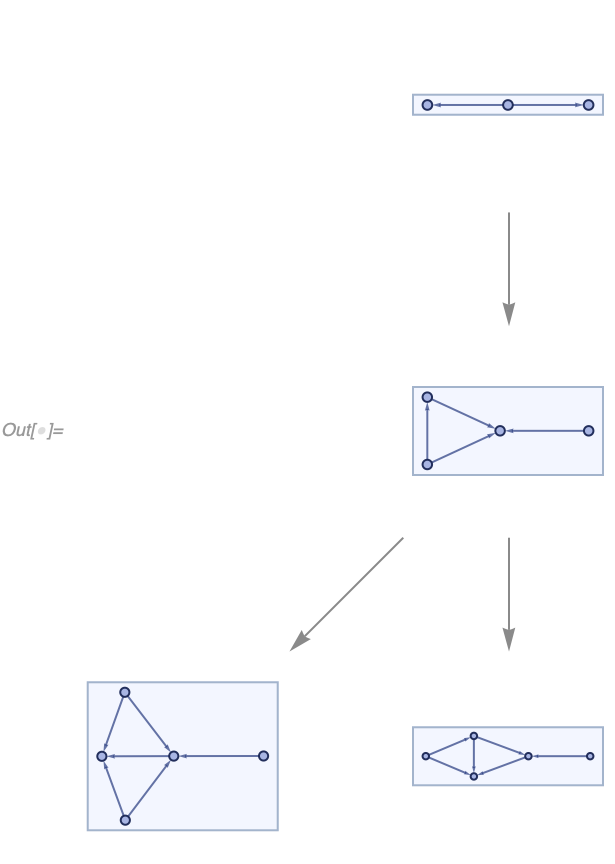
Keep in mind, evolution is not unique (as this is not a causal invariant rule):

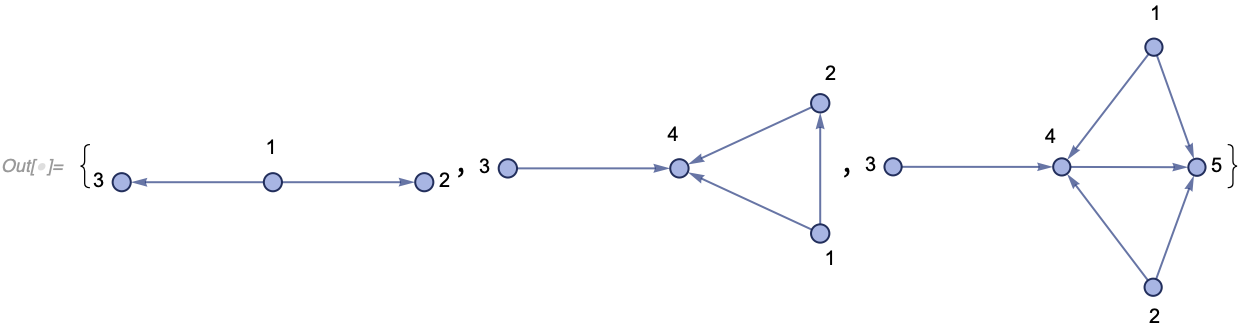
Specifically, in the default evolution order, we get the result from the paper: In[] := WolframModel[{{x, y}, {x, z}} -> {{z, w}, {y, w}, {x, w}, {x, y}}, {{1, 2}, {1, 3}}, <|"MaxEvents" -> 2|>]["StatesPlotsList", VertexLabels -> Automatic]

If, however, we use a different event ordering function, we get the evolution you found: In[] := WolframModel[{{x, y}, {x, z}} -> {{z, w}, {y, w}, {x, w}, {x, y}}, {{1, 2}, {1, 3}}, <|"MaxEvents" -> 2|>, "EventOrderingFunction" -> "ReverseRuleOrdering"]["StatesPlotsList", VertexLabels -> Automatic]

You can use MultiwaySystem to find these two are the only possibilities for the first two steps (up to isomorphisms): In[] := ResourceFunction["MultiwaySystem"][ "WolframModel" -> {{{x, y}, {x, z}} -> {{z, w}, {y, w}, {x, w}, {x, y}}}, {{{1, 2}, {1, 3}}}, 2, "StatesGraph", VertexSize -> 1.3] // LayeredGraphPlot

seem to be similar issues throughout the page - maybe just y and z got switched somewhere (or I'm being dense...)