Hi Bryan,
Try FindInstance.
Best,
David
PS. If you put your code in a spikey box we can copy/paste from it.
(Remove semicolons and evaluate)
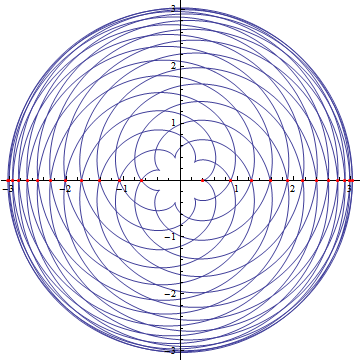
xcoordinate[a_, b_, t_] := (a + b) Cos[t] - b Cos[(a + b)/b t];
ycoordinate[a_, b_, t_] := (a + b) Sin[t] - b Sin[(a + b)/b t];
plot1 = ParametricPlot[{xcoordinate[2/5, 46/35, t],
ycoordinate[2/5, 46/35, t]}, {t, 0, 46 \[Pi]}];
(* Find t for up to 1000 instances *)
tValues =
t /. FindInstance[
ycoordinate[2/5, 46/35, t] == 0 && 0 <= t <= 46 \[Pi], {t},
Reals, 1000] // N;
(* Make points at the intercept coordinates *)
points = {Red,
Point[{xcoordinate[2/5, 46/35, #], ycoordinate[2/5, 46/35, #]}] & /@
tValues};
Show[plot1, Epilog -> points];