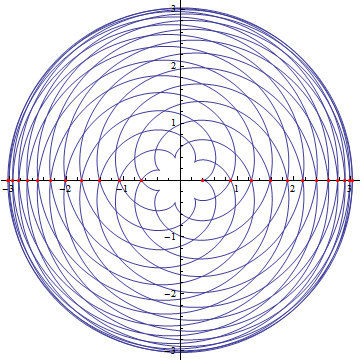
xcoordinate[a_, b_, t_] := (a + b) Cos[t] - b Cos[(a + b)/b t];
 
 ycoordinate[a_, b_, t_] := (a + b) Sin[t] - b Sin[(a + b)/b t];
 
 plot1 = ParametricPlot[{xcoordinate[2/5, 46/35, t],
     ycoordinate[2/5, 46/35, t]}, {t, 0, 46 \[Pi]}];
 
 (* Find t for up to 1000 instances *)
 tValues =
  t /. FindInstance[
     ycoordinate[2/5, 46/35, t] == 0 && 0 <= t <= 46 \[Pi], {t},
     Reals, 1000] // N;

(* Make points at the intercept coordinates *)
points = {Red,
   Point[{xcoordinate[2/5, 46/35, #], ycoordinate[2/5, 46/35, #]}] & /@
     tValues};

Show[plot1, Epilog -> points];