Improved illustrations of the interweaving grid-graphs:
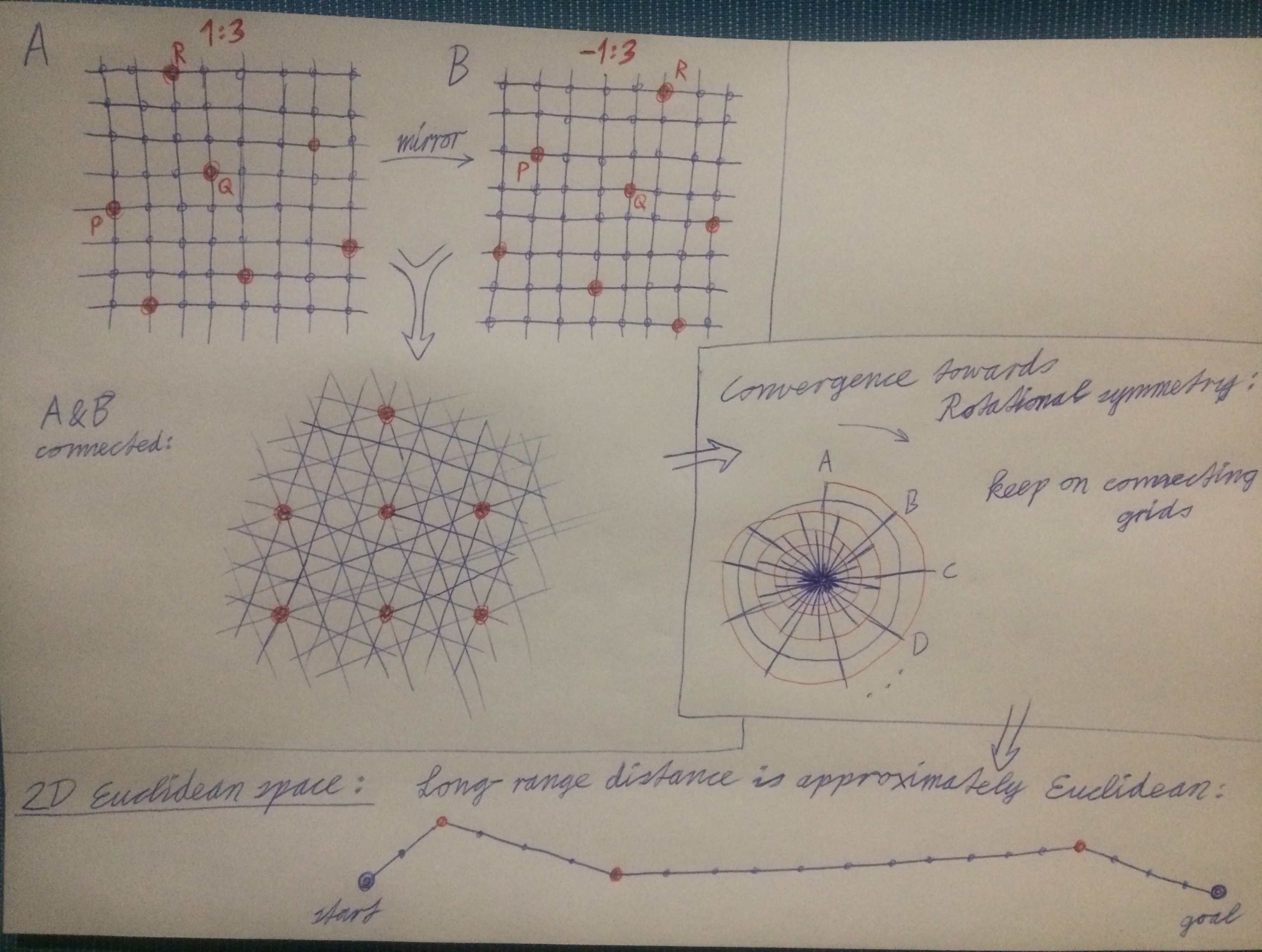
An example of how to achieve a graph from which a 2D space with Euclidean distance emerges at a large scale, and therefore rotational also symmetry:
Analogous example for a 2D SpaceTime with Lorentz symmetry:
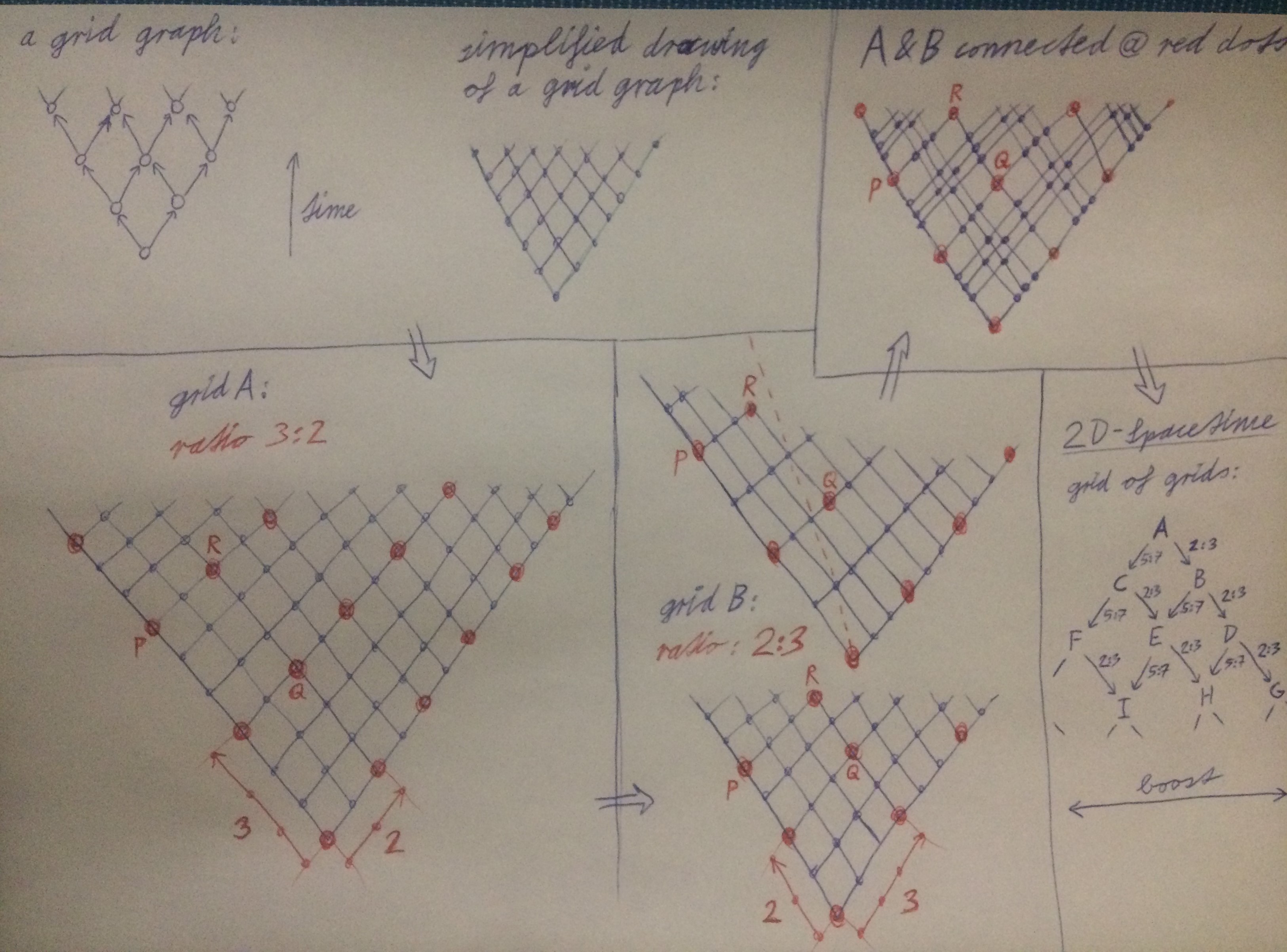
I noticed that Wolfram said in a live-stream, that you need to have random-looking connections as opposed to a grid-like structure in order to achieve the Euclidean non-Manhattan distances. But I found that you could instead just use a very large number of interweaving grids that are connected to each other in such a way that they each represent different angles of rotation while maintaining the same scale, which can actually be achieved by simple local rules on graphs. The long range graph distances would approximate Euclidean distance as the number of grids A,B,C,D... is growing. Analogous constructions can be made for a Minkowski space time, where the different grids represent frames of reference of different boosts. A very large number of such interweaving grids (called A,B,C...) then analogously leads to approximate Lorentz distance on the large scale and hence also to Lorentz symmetry. They can be arranged as a tree of girds or as a grid of grids. Note that this leads to a density of nodes that could be an astronomical number per plank cube, while the length of the edges could just be the plank length itself. Such 2D spaces that already contain rotational and Lorentz symmetries could then be used as building blocks to generate a 4D space time, but this would be more complicated and I would not be surprised if quantum phenomena emerge from these complications.