Heureka.
As far as I can see, the code does not include the idea of negations, which is why squares are created where they should not.
You are right. Negations would have prevented it.
If negations should be simulated, it would probably require some updating of the code, since the idea is not implemented yet. But they can still be used as analytical tools. And even though my example ended up being wrong, I hope that some of the ideas could still be of use. Especially the idea about subrules.
I will ask about implementing negations. It seems a good addition. Randomly generating rules with negations is harder though.
The idea about sub rules wasn't new. I already used it in previous designs, however, a few hours before you commented i learned how to express multiple rules independently: WolframModel also takes a list of rules. Your design was the correct one. My previous designs conflated the builder of "coordinate system" with the "filler of space" (r1 vs r2) which is i never ended up with a flat space.
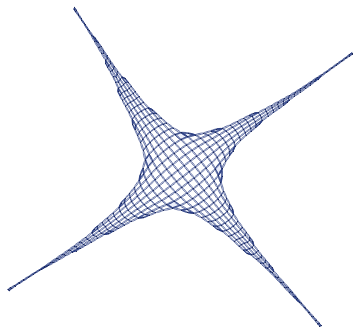
However you still got the problem of long tails.
I found it nicer to pre generate a (partial) pattern using just r1 and then fill is seperatly.
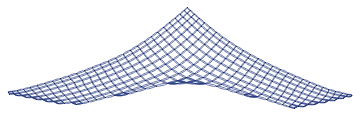
The current rules:
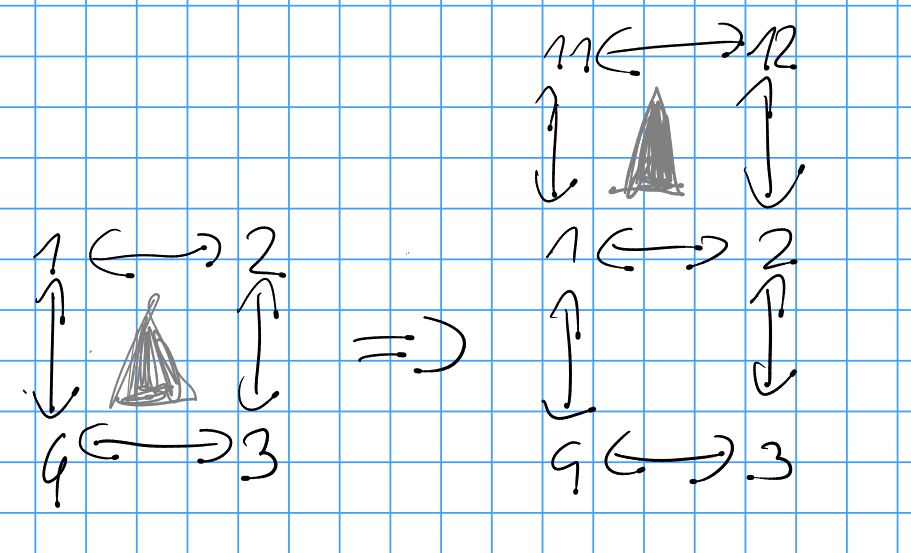
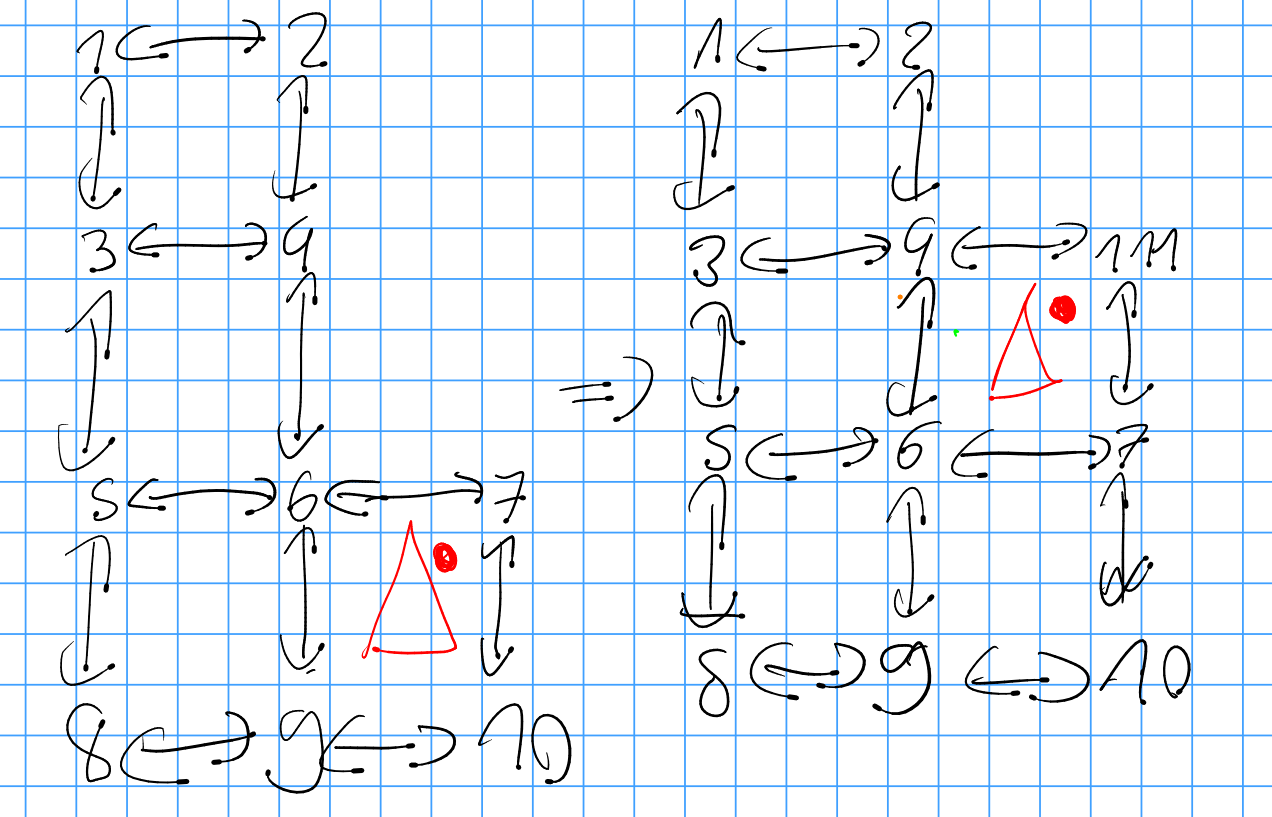
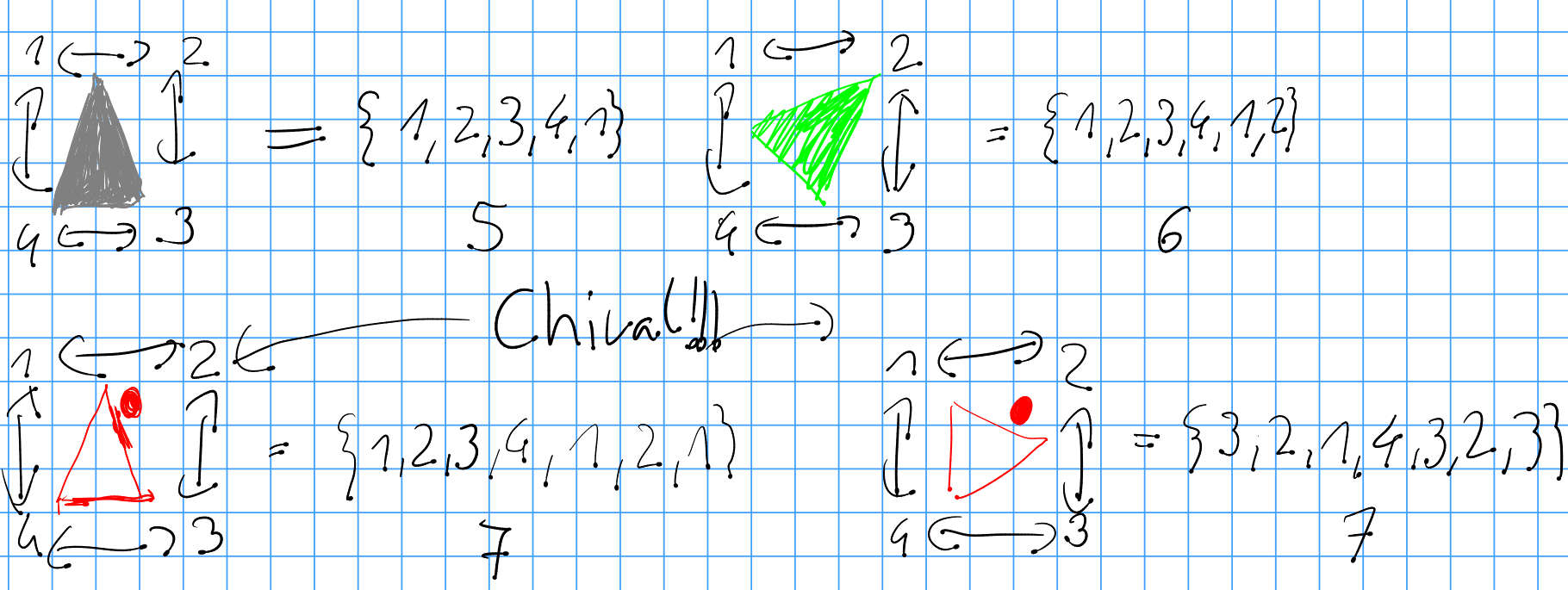
My represenations are not chiral, so i ran into problems with red, which could be solved by understanding that the problem was created by chirality.
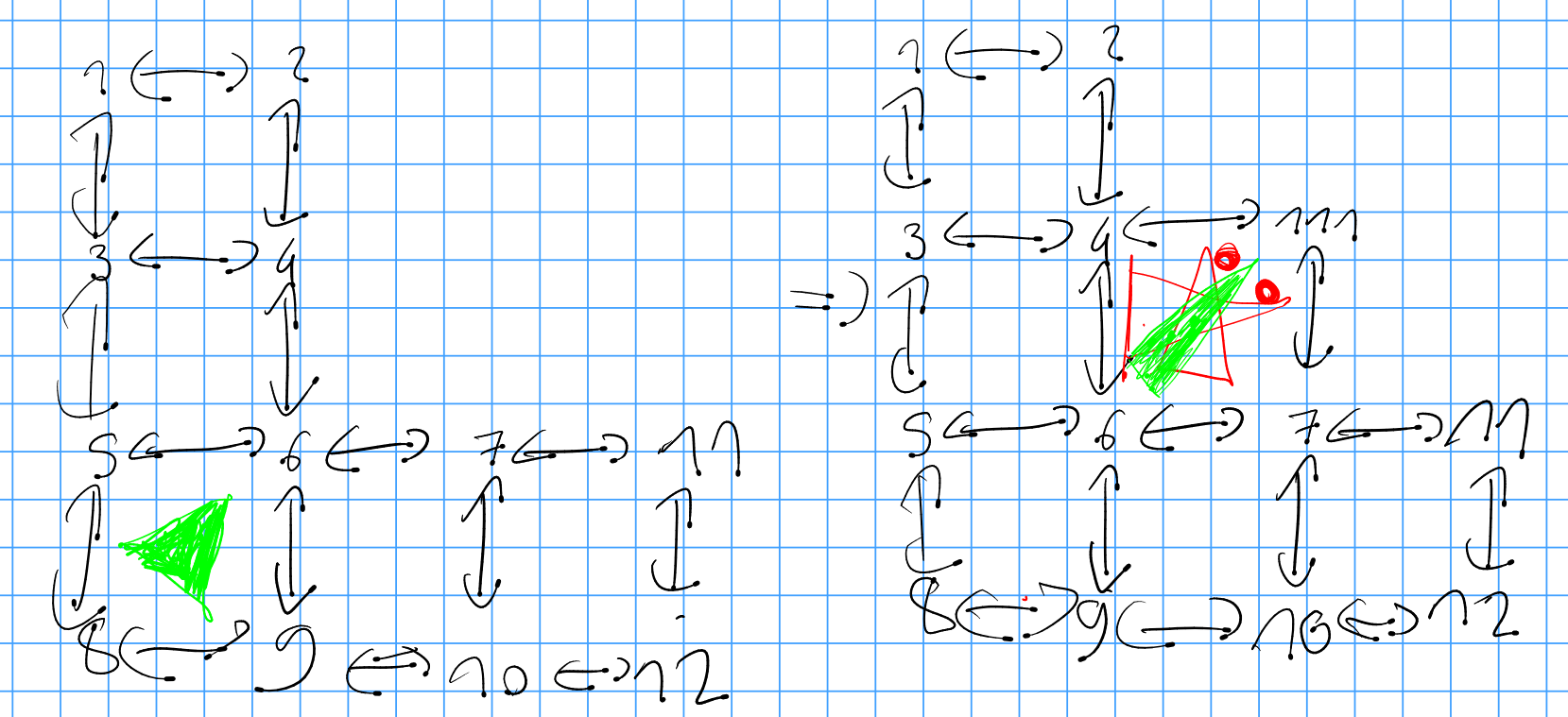
The dot always points away from the coordinate axis.
The code looks like that:
WolframModel[{
{
{5,6,9,8,5,6},
{1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
{4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
{6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
{6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
{7,11},{11,7},{11,12},{12,11},{12,10},{10,12}
} -> {
{4,111,7,6,4,111,4},
{7,111,4,6,7,111,7},
{4,111,7,6,4,111},
{1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
{4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
{6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
{6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
{7,11},{11,7},{11,12},{12,11},{12,10},{10,12},
{4,111},{111,4},{111,7},{7,111}
},
{
{6,7,10,9,6,7,6},
{1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
{4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
{6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
{6,7},{7,6},{7,10},{10,7},{10,9},{9,10}
} -> {
{4,111,7,6,4,111,4},
{1,2},{2,1},{2,4},{4,2},{4,3},{3,4},{3,1},{1,3},
{4,6},{6,4},{6,5},{5,6},{5,3},{3,5},
{6,9},{9,6},{9,8},{8,9},{8,5},{5,8},
{6,7},{7,6},{7,10},{10,7},{10,9},{9,10},
{4,111},{111,4},{111,7},{7,111}
},
{{1,2,3,4,1},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3}}->
{{11,12,2,1,11},{1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{11,1},{1,11},{11,12},{12,11},{12,2},{2,12}}
},{
{1,2,3,4,1},{2,3,4,1,2},{3,4,1,2,3},{4,1,2,3,4},
{1,2,3,4,1,2},{2,3,4,1,2,3},{3,4,1,2,3,4},{4,1,2,3,4,1},
{1,2},{2,1},{2,3},{3,2},{3,4},{4,3},{4,1},{1,4}
}
, 32, "FinalStatePlot"]
Thank You,
Malthe Andersen,
after solving this toy problem, we can strive to attack bigger problems. The solution has more potential for optimization to run faster but now we can finaly say that we can build a 2d grid.