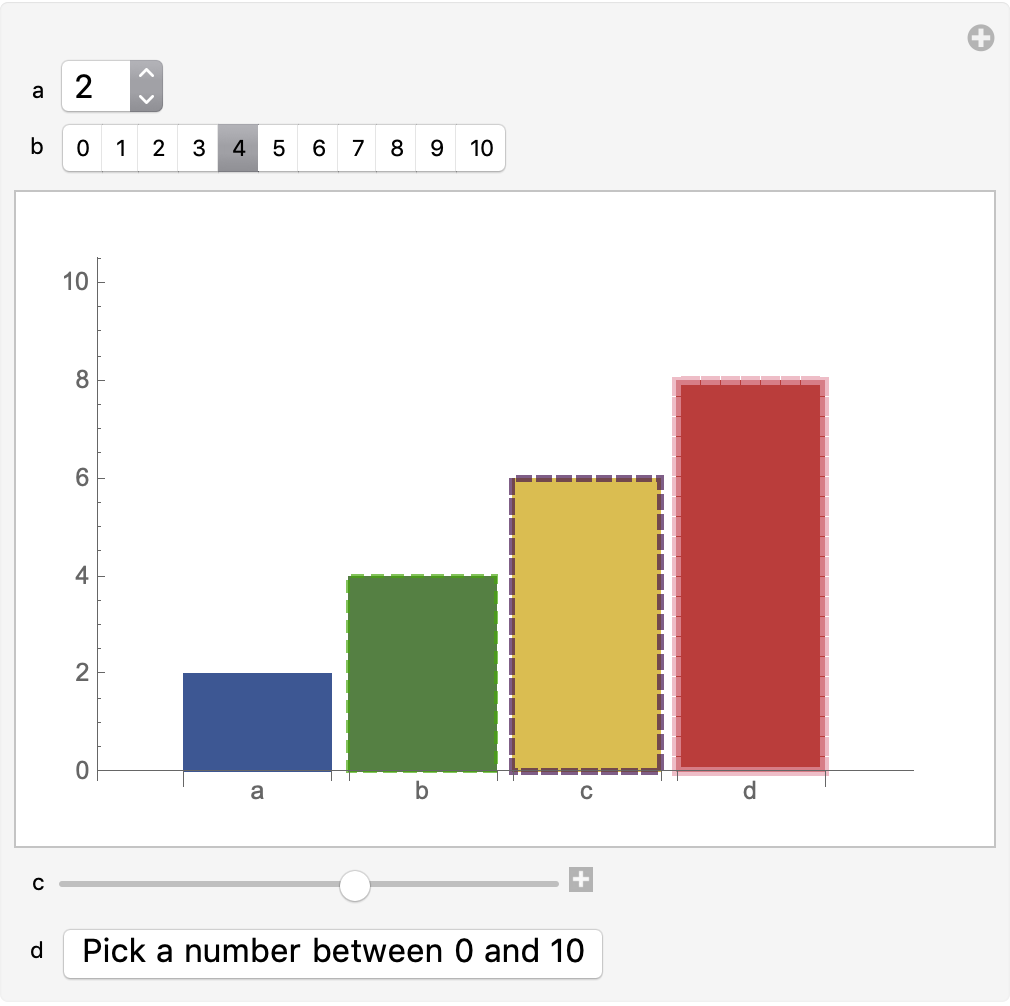
Here's mine:
Manipulate[
BarChart[{a, b, c, d}, ChartStyle -> "DarkRainbow",
ColorFunction ->
Function[{x},
Directive[ ColorData["DarkRainbow"][x],
EdgeForm[{Thickness[x/100], Dashed, RandomColor[]}]]],
ChartLabels -> {"a", "b", "c", "d"}, PlotRange -> {0, 10},
ImagePadding -> 10], {{a, 2}, Range[0, 10]}, {{b, 4}, Range[0, 10],
ControlType -> SetterBar}, {{c, 6}, 0, 10, 1}, {{d, 8},
Button["Pick a number between 0 and 10",
d = RandomInteger[{0, 10}]] &},
ControlPlacement -> {Top, Top, Bottom, Bottom}]