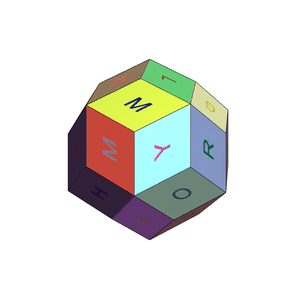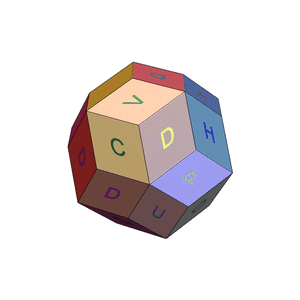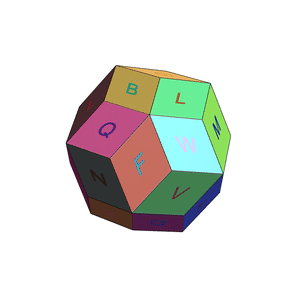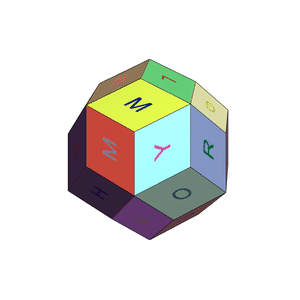
One more experiment with alphabet disco balls :)
First a function to create framed alphabets:
letter[char_String] := Framed[Style[Capitalize[char], FontSize -> 40, RandomColor[]],
Background -> Lighter[RandomColor[]], Alignment -> Center,
ImageSize -> {100, 100}, FrameStyle -> None]
Works like this:
faces = letter[#] & /@ RandomChoice[Alphabet[], 30];
faces[[1 ;; 6]] // Row

Mathematica has a built-in collection PolyhedronData[] (for creating alphabet disco balls of course), and Texture[] function to add some glitter, so I wanted to give them a try:
Texturing seems to work by using Texture[] together with Polygon's VertexTextureCoordinates property, which indicates how texture tile is mapped to the polygon. There might be a more elegant way to do this, but I ended up using ReplaceAll:
texturecoords = {{0, 0}, {1, 0}, {1, 1}, {0,
1}}; (*texture tile corners*)
polygons =
PolyhedronData["RhombicTriacontahedron", "Polygons"] /.
Polygon_[args_] :>
Polygon[args,
VertexTextureCoordinates ->
texturecoords]; (*add texturecoords to each polygon in the \
polyhedron*)
With some effort and by borrowing code and ideas from Valeriu's and Rohit's posts above, I managed to create an alphabet disco ball:
frames = Table[
Graphics3D[{Specularity[White, 20],
Table[{Texture[faces[[k]]], polygons[[k]]}, {k, 1,
Length[polygons]}]}, Boxed -> False, RotationAction -> "Clip",
ViewVector -> {10 Cos[t], 5, 20 Sin[t]}], {t, -Pi, Pi, Pi/20}];
Export["alphabet_discoball.gif", frames, "DisplayDurations" -> .2,
ImageSize -> Medium];