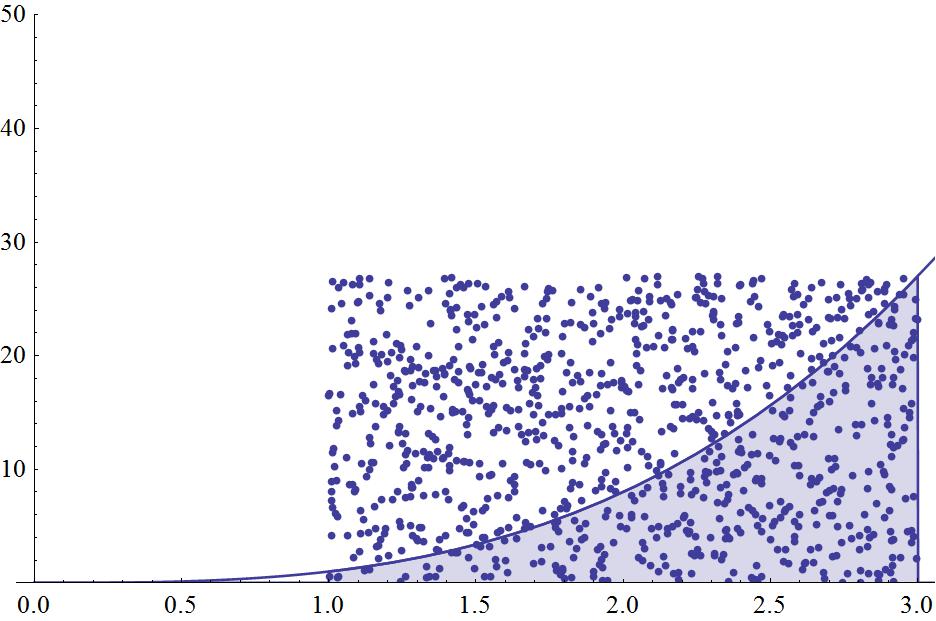
Hi Im trying to obtain the area of the function f(x)=x^3 from 1 to 3, but by aproximation with random points in a rectangle area of [1,3]X[3,27] but I can´t count the points that are inside my function only is this I need the total points that are inside my function from 1 to 3.
In mathematica I put this:
fn[x_] := If[1 < x < 3, x^3, 0]
f3 = Plot[fn[x], {x, 0, 5}, Filling -> Axis, AxesOrigin -> {0, 0},
PlotRange -> {0, 50}];
f4 = Show[f3, Plot[x^3, {x, 0, 10}], AxesLabel -> {"x", "y"},
PlotLabel -> "y=x^3"]
nlist = 1000;
For[i = 1, i <= nlist, i++, z[i] = RandomReal[{1, 3}];]
For[i = 1, i <= nlist, i++, w[i] = RandomReal[{0, 27}];]
u = Table[{z[i], w[i]}, {i, 1, nlist}];
ranpa = ListPlot[u, AxesOrigin -> {0, 0}, PlotRange -> {0, 50}]
Show[ranpa, f4]
Someone told that is using If and Do, but a can´t find out how.
Thanks!