Hi,
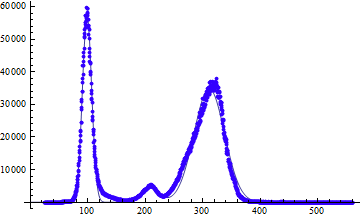
Is it some kind of photon distribution? If you split your problem into parts result will look slightly better.
model1 = (amp1 E^(-((-mu1 + x)^2/(2 sigma1^2))));
model2 = (amp2 E^(-((-mu2 + x)^2/(2 sigma2^2))));
model3 = (amp3 E^(-((-mu3 + x)^2/(2 sigma3^2))));
vars1 = {{amp1, 63000}, {mu1, 100}, {sigma1}};
vars2 = {{amp2, 6000}, {mu2, 210}, {sigma2}};
vars3 = {{amp3, 40000}, {mu3, 310}, {sigma3}};
fit1 = NonlinearModelFit[data1, {model1, amp1 > 0 && sigma1 > 0}, vars1, x, MaxIterations -> 100];
fit2 = NonlinearModelFit[data2, {model2, amp2 > 0 && sigma2 > 0}, vars2, x, MaxIterations -> 100];
fit3 = NonlinearModelFit[data3, {model3, amp3 > 0 && sigma3 > 0}, vars3, x, MaxIterations -> 100];
Show[
Plot[{fit1[x] + fit2[x] + fit3[x]}, {x, 0, 500}, PlotRange -> All],
ListPlot[data, PlotStyle -> {AbsolutePointSize[4], Hue[.7]},
PlotRange -> {{0, 400}, {0, 65000}}]
]
Sorry, I forgot to add definitions for data1,data2 and data3,
each of them in fact something like Take[data,{n,m}] where n&m are chosen so that data looks like gaussian in that range.
I've already removed exact ranges, but I still have them loaded into memory, so here are the files
http://sharesend.com/h35pjd31 - d3.txt
http://sharesend.com/0faxgkcx - d2.txt
http://sharesend.com/att5y5vc - d1.txt
I.M.