Hello all!
My favorite Wolfram Language function is Manipulate because it is simply one of the best ways to show young people how patterns develop and change.
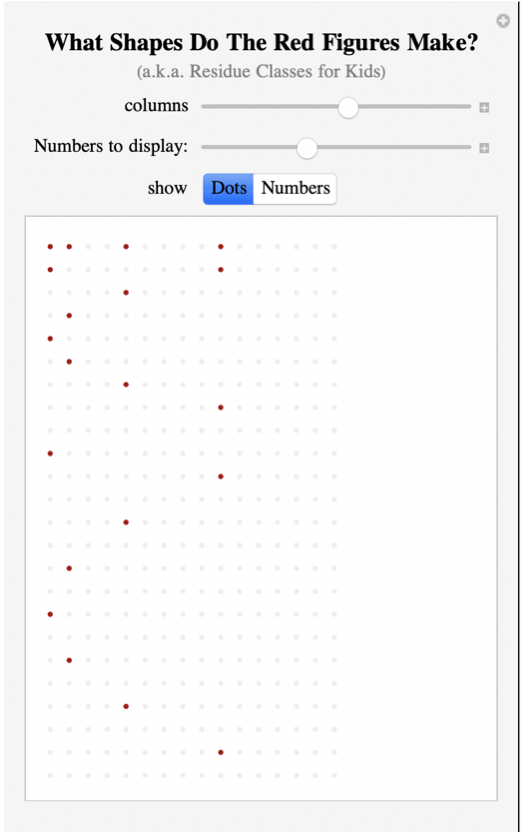
This code is inspired by John. H. Conway (1937-2020), Richard K. Guy (1916-2020) in their Book of Numbers (Springer-Verlag 1996, page 31, Figure 2.10).
ENJOY!
Manipulate[Multicolumn[show[n], columns, Appearance -> "Horizontal"],
{{columns, 10}, 5, 25, 1}, {{n, 25, "Numbers to display:"}, 5, 1000,
1}, {show, {redDots -> "Dots", redSquares -> "Numbers"}},
LabelStyle -> {14, FontFamily -> "Times"},
FrameLabel -> {"", "",
Column[{Style["What Shapes Do The Red Figures Make?", Bold, 18],
Style["(a.k.a. Residue Classes for Kids)", Gray]},
Alignment -> Center], ""},
Initialization :> {
tinyCircRed =
Graphics[{Darker@Red, Disk[{0, 0}, .01]}, ImageSize -> 5],
tinyCircGray =
Graphics[{Lighter@RGBColor[.9, .9, .9], Disk[{0, 0}, .01]},
ImageSize -> 5],
redSquares[max_] := Table[
If[IntegerQ[Sqrt[x]] == True,
Style[x, Darker@Red, 16, Bold, FontFamily -> "Times"],
Style[x, Lighter@Gray]], {x, 1, max, 1}],
redDots[max_] := Table[
If[IntegerQ[Sqrt[x]] == True, tinyCircRed, tinyCircGray], {x, 0,
max, 1}]}]