I try to solve this Simple symmetric continuum mechanical problem but I'm getting different solutions 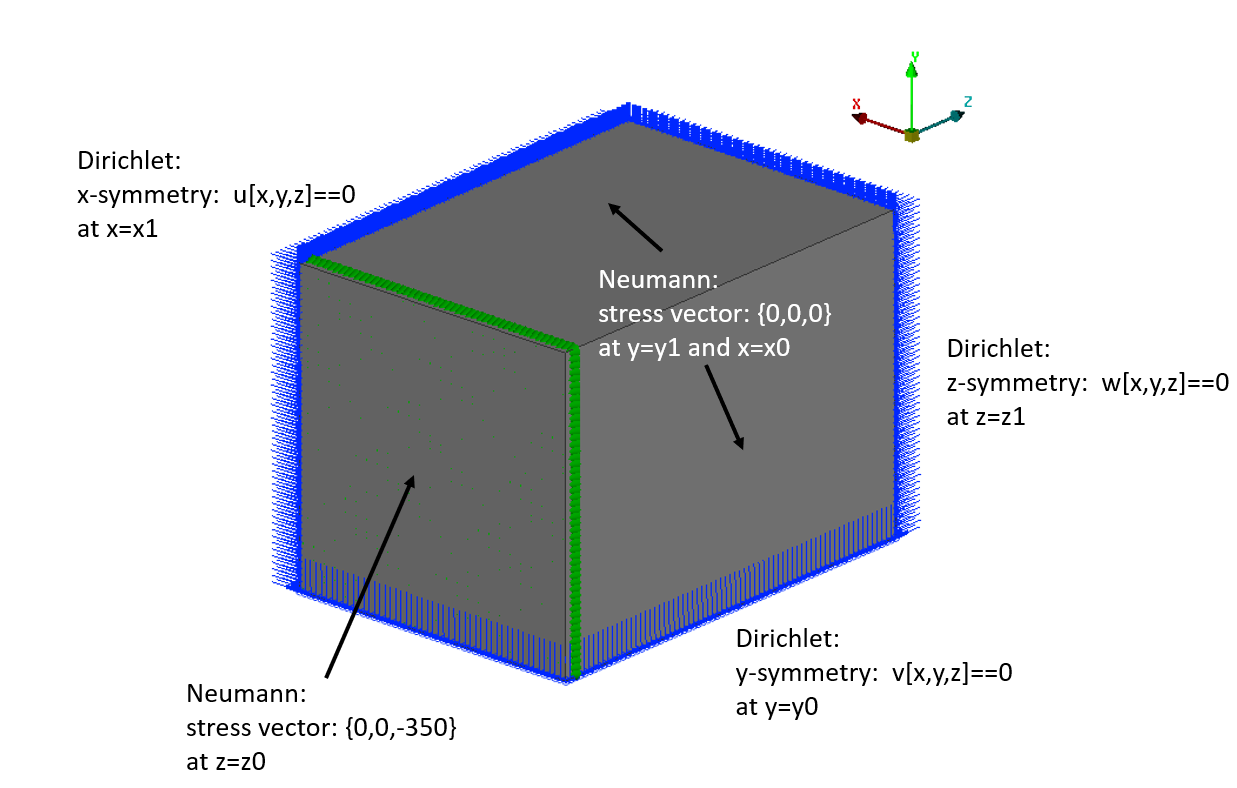
PDE in Inactive operator form
Operator-Form from documentation example: https://reference.wolfram.com/language/FEMDocumentation/tutorial/FiniteElementBestPractice.html
op = {Inactive[
Div][({{0, 0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu])))}, {0, 0,
0}, {-(Y/(2 (1 + \[Nu]))), 0, 0}}.Inactive[Grad][
w[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))),
0}, {-(Y/(2 (1 + \[Nu]))), 0, 0}, {0, 0, 0}}.Inactive[Grad][
v[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{-((Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu]))), 0,
0}, {0, -(Y/(2 (1 + \[Nu]))), 0}, {0,
0, -(Y/(2 (1 + \[Nu])))}}.Inactive[Grad][
u[x, y, z], {x, y, z}]), {x, y, z}],
Inactive[
Div][({{0, 0, 0}, {0,
0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu])))}, {0, -(Y/(
2 (1 + \[Nu]))), 0}}.Inactive[Grad][
w[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{0, -(Y/(2 (1 + \[Nu]))),
0}, {-((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0, 0}, {0, 0,
0}}.Inactive[Grad][u[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{-(Y/(2 (1 + \[Nu]))), 0,
0}, {0, -((Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu]))),
0}, {0, 0, -(Y/(2 (1 + \[Nu])))}}.Inactive[Grad][
v[x, y, z], {x, y, z}]), {x, y, z}],
Inactive[
Div][({{0, 0, 0}, {0,
0, -(Y/(2 (1 + \[Nu])))}, {0, -((
Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0}}.Inactive[Grad][
v[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{0, 0, -(Y/(2 (1 + \[Nu])))}, {0, 0,
0}, {-((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0,
0}}.Inactive[Grad][u[x, y, z], {x, y, z}]), {x, y, z}] +
Inactive[
Div][({{-(Y/(2 (1 + \[Nu]))), 0, 0}, {0, -(Y/(2 (1 + \[Nu]))),
0}, {0, 0, -((
Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu])))}}.Inactive[
Grad][w[x, y, z], {x, y, z}]), {x, y, z}]} /. {Y ->
210000, \[Nu] -> 3/10};
Domain (a simple block, c.f. Figure):
x0 = 0; x1 = 50;
y0 = 0; y1 = 50;
z0 = 0; z1 = 70;
Symmetric boundary conditions and given stress value:
\[CapitalGamma]Xsym = DirichletCondition[{u[x, y, z] == 0}, x == x1];
\[CapitalGamma]Ysym = DirichletCondition[{v[x, y, z] == 0}, y == y0];
\[CapitalGamma]Zsym = DirichletCondition[{w[x, y, z] == 0}, z == z1];
(* Stress component in z-direction Subscript[\[Sigma], zz], Neumann \
boundary condition*)
stress = 350;
{uifWL, vifWL, wifWL} =
NDSolveValue[{op == {0,
0, -NeumannValue[stress,
z == z0]}, \[CapitalGamma]Xsym, \[CapitalGamma]Ysym, \
\[CapitalGamma]Zsym}, {u, v, w}, {x, x0, x1}, {y, y0, y1}, {z, z0,
z1}]
Show the result
Define stress tensor depending on the displacements u,v,w:
\[Nu] = 3/10; g = 210000/(2 (1 + \[Nu])); (* material constants*)
e = Subscript[\[Epsilon], xx] + Subscript[\[Epsilon], yy] +
Subscript[\[Epsilon], zz];
Subscript[\[Sigma], xx] =
2 g (Subscript[\[Epsilon],
xx] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], xy] =
g Subscript[\[Gamma], xy];
Subscript[\[Sigma], yy] =
2 g (Subscript[\[Epsilon],
yy] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], xz] =
g Subscript[\[Gamma], xz];
Subscript[\[Sigma], zz] =
2 g (Subscript[\[Epsilon],
zz] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], yz] =
g Subscript[\[Gamma], yz];
stressTensor = ( {
{Subscript[\[Sigma], xx], Subscript[\[Tau], xy], Subscript[\[Tau],
xz]},
{Subscript[\[Tau], xy], Subscript[\[Sigma], yy], Subscript[\[Tau],
yz]},
{Subscript[\[Tau], xz], Subscript[\[Tau], yz], Subscript[\[Sigma],
zz]}
} ) /. {Subscript[\[Epsilon], xx] ->
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Epsilon], yy] ->
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Epsilon], zz] ->
\!\(\*SuperscriptBox[\(w\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], xy] ->
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], xz] ->
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(w\),
TagBox[
RowBox[{"(",
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], yz] ->
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] +
\!\(\*SuperscriptBox[\(w\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z]}
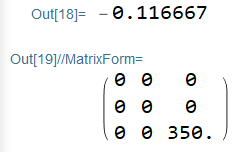
The solution is correct:
wifWL[0, 0, z0] (* displacement in z-direction *)
(stressTensor /. {u -> uifWL, v -> vifWL, w -> wifWL} /. {x -> 25,
y -> 25, z -> z0}) // Chop[#, 10^-9] & // MatrixForm
Same PDE and boundaries just with Active operator form gives a different (incorrect ) solution
opActive = Activate[op]
NDSolveValue[{opActive == {0,
0, -NeumannValue[stress,
z == z0]}, \[CapitalGamma]Xsym, \[CapitalGamma]Ysym, \
\[CapitalGamma]Zsym}, {u, v, w}, {x, x0, x1}, {y, y0, y1}, {z, z0,
z1}];
%[[3]][0, 0, z0]
(stressTensor /. {u -> %%[[1]], v -> %%[[2]], w -> %%[[3]]} /. {x ->
25, y -> 25, z -> z0}) // Chop[#, 10^-9] & // MatrixForm

Comment: According to Wolfram Language documentation:
This is due to the different interpretation of the "Coefficient Form of a PDE" in Inactive and Active operator form in conjunction with the Neumann[] boundary condition; see explanations in
https://reference.wolfram.com/language/FEMDocumentation/tutorial/FiniteElementBestPractice.html https://ipfs-sec.stackexchange.cloudflare-ipfs.com/mathematica/A/question/100455.html
This means that such formulations, which contain Neumann[] boundary conditions, must always be formulated with the Inactivated operator representation.
1. Question: Is there a possibility to solve a PDE in the Active operator form with Neumann boundary conditions in such a way that the boundary conditions are correctly considered (I would like to avoid the Inactive form)?
First approach avoidance of NeumannValue[] and DirichletCondition[]-Function instead direct input of all boundary conditions
Neumann boundaries in direct Form:
boundaryNeumannInDirectForm = {
(stressTensor.{0, 1, 0} == {0, 0, 0} /. y -> y1) // Thread,
(stressTensor.{-1, 0, 0} == {0, 0, 0} /. x -> x0) // Thread,
(stressTensor.{0, 0, -1} == {0, 0, -stress} /. z -> z0) // Thread
} // Simplify // Flatten
Dirichlet boundaries in direct Form:
boundaryDirichletInDirectForm = {
u[x, y, z] == 0 /. x -> x1, v[x, y, z] == 0 /. y -> y0,
w[x, y, z] == 0 /. z -> z1
}
NDSolveValue gives an error:
NDSolveValue[{(opActive == {0, 0, 0}) // Thread,
Flatten@{boundaryDirichletInDirectForm,
boundaryNeumannInDirectForm}}, {u, v, w}, {x, x0, x1}, {y, y0,
y1}, {z, z0, z1}]

2. Question: What's the problem here, with the direct formulation? Why does WL interpret the Neumann boundary conditions as Dirichlet boundary conditions and how can this be avoided?
A similar example from the WL-Documentation seems to work:
pde = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\((\((v[t, x] - 1)\)\
\*SubscriptBox[\(\[PartialD]\), \(x\)]u[t, x])\)\) + (16 x t - 2 t -
16 (v[t, x] - 1)) (u[t, x] - 1) + 10 x E^(-4 x), \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(v[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(v[t, x]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\(u[t, x]\)\) + 4 u[t, x] - 4 +
x^2 - 2 t - 10 t E^(-4 x)};
bc = {u[0, x] == 1, v[0, x] == 1, u[t, 0] == 1, v[t, 0] == 1,
3 u[t, 1] +
\!\(\*SuperscriptBox[\(u\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[t, 1] == 3, 5
\!\(\*SuperscriptBox[\(v\),
TagBox[
RowBox[{"(",
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[t, 1] == E^4 (u[t, 1] - 1)};
NDSolve[{pde, bc}, {u, v}, {x, 0, 1}, {t, 0, 2}]
For easier use I have attached the wl file.
Many thanks for the help
 Attachments:
Attachments: