Group Abstract Group Abstract

Message Boards Message Boards

Questions about NDSolve with Dirichlet/Neumann bcs and direct formulations

I try to solve this Simple symmetric continuum mechanical problem but I'm getting different solutions 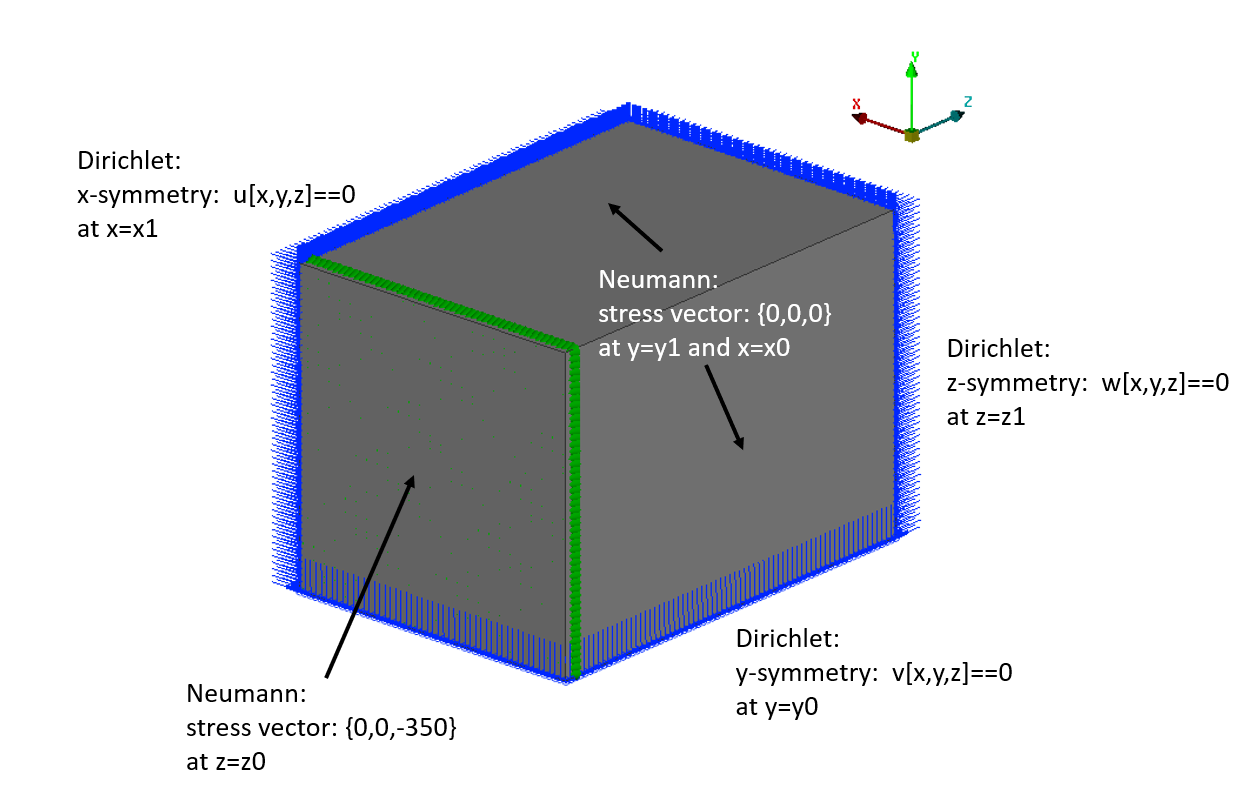A Simple symmetric continuum mechanical Problem

PDE in Inactive operator form

Operator-Form from documentation example: https://reference.wolfram.com/language/FEMDocumentation/tutorial/FiniteElementBestPractice.html

op = {Inactive[
       Div][({{0, 0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu])))}, {0, 0,
           0}, {-(Y/(2 (1 + \[Nu]))), 0, 0}}.Inactive[Grad][
         w[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 
          0}, {-(Y/(2 (1 + \[Nu]))), 0, 0}, {0, 0, 0}}.Inactive[Grad][
         v[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{-((Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu]))), 0, 
          0}, {0, -(Y/(2 (1 + \[Nu]))), 0}, {0, 
          0, -(Y/(2 (1 + \[Nu])))}}.Inactive[Grad][
         u[x, y, z], {x, y, z}]), {x, y, z}], 
    Inactive[
       Div][({{0, 0, 0}, {0, 
          0, -((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu])))}, {0, -(Y/(
           2 (1 + \[Nu]))), 0}}.Inactive[Grad][
         w[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{0, -(Y/(2 (1 + \[Nu]))), 
          0}, {-((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0, 0}, {0, 0,
           0}}.Inactive[Grad][u[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{-(Y/(2 (1 + \[Nu]))), 0, 
          0}, {0, -((Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu]))), 
          0}, {0, 0, -(Y/(2 (1 + \[Nu])))}}.Inactive[Grad][
         v[x, y, z], {x, y, z}]), {x, y, z}], 
    Inactive[
       Div][({{0, 0, 0}, {0, 
          0, -(Y/(2 (1 + \[Nu])))}, {0, -((
           Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0}}.Inactive[Grad][
         v[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{0, 0, -(Y/(2 (1 + \[Nu])))}, {0, 0, 
          0}, {-((Y \[Nu])/((1 - 2 \[Nu]) (1 + \[Nu]))), 0, 
          0}}.Inactive[Grad][u[x, y, z], {x, y, z}]), {x, y, z}] + 
     Inactive[
       Div][({{-(Y/(2 (1 + \[Nu]))), 0, 0}, {0, -(Y/(2 (1 + \[Nu]))), 
          0}, {0, 0, -((
           Y (1 - \[Nu]))/((1 - 2 \[Nu]) (1 + \[Nu])))}}.Inactive[
          Grad][w[x, y, z], {x, y, z}]), {x, y, z}]} /. {Y -> 
     210000, \[Nu] -> 3/10};

Domain (a simple block, c.f. Figure):

x0 = 0; x1 = 50; 
y0 = 0; y1 = 50;
z0 = 0; z1 = 70;

Symmetric boundary conditions and given stress value:

\[CapitalGamma]Xsym = DirichletCondition[{u[x, y, z] == 0}, x == x1];
\[CapitalGamma]Ysym = DirichletCondition[{v[x, y, z] == 0}, y == y0];
\[CapitalGamma]Zsym = DirichletCondition[{w[x, y, z] == 0}, z == z1];
(* Stress component in z-direction Subscript[\[Sigma], zz], Neumann \
boundary condition*)
stress = 350;

{uifWL, vifWL, wifWL} = 
 NDSolveValue[{op == {0, 
     0, -NeumannValue[stress, 
       z == z0]}, \[CapitalGamma]Xsym, \[CapitalGamma]Ysym, \
\[CapitalGamma]Zsym}, {u, v, w}, {x, x0, x1}, {y, y0, y1}, {z, z0, 
   z1}]

Show the result

Define stress tensor depending on the displacements u,v,w:

\[Nu] = 3/10; g = 210000/(2 (1 + \[Nu])); (* material constants*)
e = Subscript[\[Epsilon], xx] + Subscript[\[Epsilon], yy] + 
   Subscript[\[Epsilon], zz];
Subscript[\[Sigma], xx] = 
 2 g (Subscript[\[Epsilon], 
    xx] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], xy] = 
 g Subscript[\[Gamma], xy];
Subscript[\[Sigma], yy] = 
 2 g (Subscript[\[Epsilon], 
    yy] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], xz] = 
 g Subscript[\[Gamma], xz];
Subscript[\[Sigma], zz] = 
 2 g (Subscript[\[Epsilon], 
    zz] + \[Nu]/(1 - 2 \[Nu]) e); Subscript[\[Tau], yz] = 
 g Subscript[\[Gamma], yz];

stressTensor = ( {
    {Subscript[\[Sigma], xx], Subscript[\[Tau], xy], Subscript[\[Tau],
      xz]},
    {Subscript[\[Tau], xy], Subscript[\[Sigma], yy], Subscript[\[Tau],
      yz]},
    {Subscript[\[Tau], xz], Subscript[\[Tau], yz], Subscript[\[Sigma],
      zz]}
   } ) /. {Subscript[\[Epsilon], xx] -> 
\!\(\*SuperscriptBox[\(u\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Epsilon], yy] -> 
\!\(\*SuperscriptBox[\(v\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Epsilon], zz] -> 
\!\(\*SuperscriptBox[\(w\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], xy] -> 
\!\(\*SuperscriptBox[\(u\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] + 
\!\(\*SuperscriptBox[\(v\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], xz] -> 
\!\(\*SuperscriptBox[\(u\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] + 
\!\(\*SuperscriptBox[\(w\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z], Subscript[\[Gamma], yz] -> 
\!\(\*SuperscriptBox[\(v\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z] + 
\!\(\*SuperscriptBox[\(w\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y, z]}

The solution is correct:

wifWL[0, 0, z0] (* displacement in z-direction *)
(stressTensor /. {u -> uifWL, v -> vifWL, w -> wifWL} /. {x -> 25, 
     y -> 25, z -> z0}) // Chop[#, 10^-9] & // MatrixForm

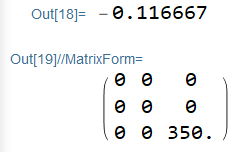
correct Solution

Same PDE and boundaries just with Active operator form gives a different (incorrect ) solution

opActive = Activate[op]
NDSolveValue[{opActive == {0, 
     0, -NeumannValue[stress, 
       z == z0]}, \[CapitalGamma]Xsym, \[CapitalGamma]Ysym, \
\[CapitalGamma]Zsym}, {u, v, w}, {x, x0, x1}, {y, y0, y1}, {z, z0, 
   z1}];

%[[3]][0, 0, z0]
(stressTensor /. {u -> %%[[1]], v -> %%[[2]], w -> %%[[3]]} /. {x -> 
      25, y -> 25, z -> z0}) // Chop[#, 10^-9] & // MatrixForm

incorrect result

Comment: According to Wolfram Language documentation:

This is due to the different interpretation of the "Coefficient Form of a PDE" in Inactive and Active operator form in conjunction with the Neumann[] boundary condition; see explanations in

https://reference.wolfram.com/language/FEMDocumentation/tutorial/FiniteElementBestPractice.html https://ipfs-sec.stackexchange.cloudflare-ipfs.com/mathematica/A/question/100455.html

This means that such formulations, which contain Neumann[] boundary conditions, must always be formulated with the Inactivated operator representation.

1. Question: Is there a possibility to solve a PDE in the Active operator form with Neumann boundary conditions in such a way that the boundary conditions are correctly considered (I would like to avoid the Inactive form)?

First approach avoidance of NeumannValue[] and DirichletCondition[]-Function instead direct input of all boundary conditions

Neumann boundaries in direct Form:

boundaryNeumannInDirectForm = {
    (stressTensor.{0, 1, 0} == {0, 0, 0} /. y -> y1) // Thread,
    (stressTensor.{-1, 0, 0} == {0, 0, 0} /. x -> x0) // Thread,
    (stressTensor.{0, 0, -1} == {0, 0, -stress} /. z -> z0) // Thread
    } // Simplify // Flatten

Dirichlet boundaries in direct Form:

boundaryDirichletInDirectForm = {
  u[x, y, z] == 0 /. x -> x1, v[x, y, z] == 0 /. y -> y0, 
  w[x, y, z] == 0 /. z -> z1
  }

NDSolveValue gives an error:

NDSolveValue[{(opActive == {0, 0, 0}) // Thread, 
  Flatten@{boundaryDirichletInDirectForm, 
    boundaryNeumannInDirectForm}}, {u, v, w}, {x, x0, x1}, {y, y0, 
  y1}, {z, z0, z1}]

enter image description here

2. Question: What's the problem here, with the direct formulation? Why does WL interpret the Neumann boundary conditions as Dirichlet boundary conditions and how can this be avoided?

A similar example from the WL-Documentation seems to work:

pde = {\!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(u[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\((\((v[t, x] - 1)\)\ 
\*SubscriptBox[\(\[PartialD]\), \(x\)]u[t, x])\)\) + (16 x t - 2 t - 
        16 (v[t, x] - 1)) (u[t, x] - 1) + 10 x E^(-4 x), \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(v[t, x]\)\) == \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(v[t, x]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \(x\)]\(u[t, x]\)\) + 4 u[t, x] - 4 + 
     x^2 - 2 t - 10 t E^(-4 x)};
bc = {u[0, x] == 1, v[0, x] == 1, u[t, 0] == 1, v[t, 0] == 1, 
   3 u[t, 1] + 
\!\(\*SuperscriptBox[\(u\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[t, 1] == 3, 5 
\!\(\*SuperscriptBox[\(v\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[t, 1] == E^4 (u[t, 1] - 1)};
NDSolve[{pde, bc}, {u, v}, {x, 0, 1}, {t, 0, 2}]

For easier use I have attached the wl file.

Many thanks for the help

Attachments:
ndsolvePDE.nb
POSTED BY: Lars Ulke-Winter
2 Replies
Sort By:

Thank you very much for the answer, but what does this mean in this code example:

pde = {-(1050000/13) D[u[x, y, z], z, z] - 
    1050000/13 D[u[x, y, z], y, y] - 2625000/13 D[w[x, y, z], x, z] - 
    2625000/13 D[ v[x, y, z], x, y] - 
    3675000/13 D[u[x, y, z], x, x] == 
   0, -(1050000/13) D[v[x, y, z], z, z] - 
    2625000/13 D[w[x, y, z], y, z] - 3675000/13 D[v[x, y, z], y, y] - 
    2625000/13 D[u[x, y, z], x, y] - 1050000/13 D[v[x, y, z], x, x] ==
    0,
  -(3675000/13) D[ w[x, y, z], z, z] - 
    2625000/13 D[v[x, y, z], y, z] - 1050000/13 D[w[x, y, z], y, y] - 
    2625000/13 D[u[x, y, z], x, z] - 1050000/13 D[w[x, y, z], x, x] ==
    0}

bcs =
 (* 3 Dirichtlet bcs *)
 {u[50, y, z] == 0,
  v[x, 0, z] == 0,
  w[x, y, 70] == 0,
  (* 9 Neumann bcs*)
  (D[u[x, y, z], y] + D[v[x, y, z], x] == 0) /. {y -> 50},
  (3 D[w[x, y, z], z] + 7 D[v[x, y, z], y] + 3 D[u[x, y, z], x] == 
     0) /. {y -> 50},
  (D[v[x, y, z], z] + D[w[x, y, z], y] == 0) /. {y -> 50},
  (3 D[w[x, y, z], z] + 3 D[v[x, y, z], y] + 7 D[u[x, y, z], x] == 
     0) /. {x -> 0},
  (D[u[x, y, z], y] + D[v[x, y, z], x] == 0) /. {x -> 0},
  (D[u[x, y, z], z] + D[w[x, y, z], x] == 0) /. {x -> 0},
  (D[u[x, y, z], z] + D[w[x, y, z], x] == 0) /. {z -> 0},
  (D[v[x, y, z], z] + D[w[x, y, z], y] == 0) /. {z -> 0},
  (10500 D[w[x, y, z], z] + 4500 D[v[x, y, z], y] + 
      4500 D[u[x, y, z], x] == 13) /. z -> 0}

NDSolveValue[{pde, bcs}, {u, v, w}, {x, 0, 50}, {y, 0, 50}, {z, 0, 
  70}]

I don't understand the error message here (it is not a Dirichlet boundary condition): Error Message

Attachments:
ndSolvePDE-direct.nb
POSTED BY: Lars Ulke-Winter
Anonymous User
Anonymous User
Posted 5 years ago
POSTED BY: Anonymous User
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard