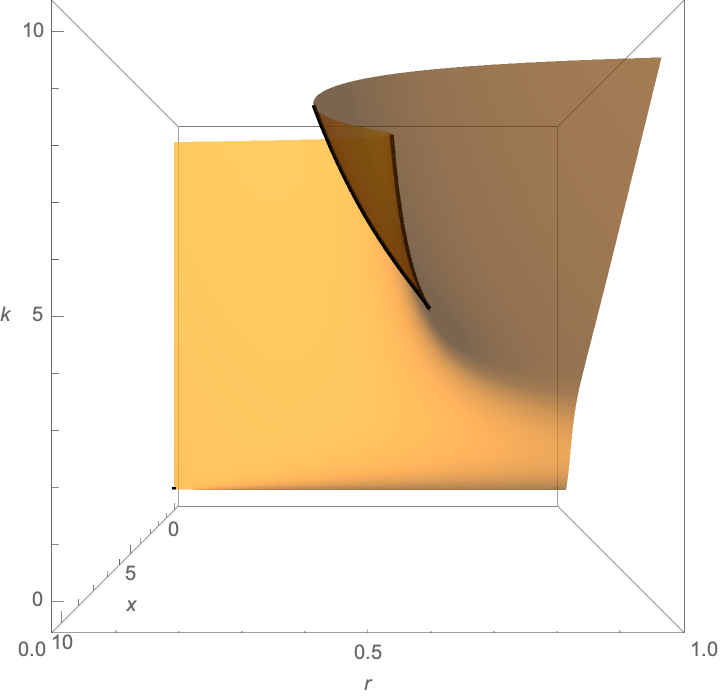
Another way, highlighting the bifurcation:

ParametricPlot3D[
 Evaluate@{r /. First@Solve[r x (1 - x/k) - x^2/(1 + x^2) == 0, r], k, x},
 {k, 0, 10}, {x, 0 + 2 $MachineEpsilon, k - 20 $MachineEpsilon}, 
 PlotPoints -> 75, MaxRecursion -> 3, 
 Method -> {"BoundaryOffset" -> False}, BoxRatios -> {1, 1, 1}, 
 PlotRange -> {{0, 1}, Automatic, Automatic},
 MeshFunctions -> {Function[{r, k, x, u, v}, 
    Last@Normalize@D[r x (1 - x/k) - x^2/(1 + x^2), {{r, k, x}}] // 
     Evaluate]}, Mesh -> {{0}}, PlotStyle -> Opacity[0.7], 
 MeshStyle -> Thick, AxesLabel -> {r, k, x}, ViewPoint -> Above]

The surface in either demo or Strogatz’s book is the contour for r-h-x space in terms of the fixed point equation, So you only need G[r,k,x] at zero.