This is a short demo with short code. Use the following utility function to find intersection of lines. The diagram shows the convention of the choice of vertices.

segmentIntersection[p1_List, p2_List, p3_List, p4_List] := 
 Block[{u, v}, Module[{sol}, 
   sol = Solve[u*(p2 - p1) + p1 == v*(p4 - p3) + p3, {u, v}];
   {u, v, u*(p2 - p1) + p1} /. sol[[1]]]]

Define a function of points on conic (or hyperbola)

pt[t_] := {m*Cos[t], n*Sin[t]}
(* pt2[t_] = {m*Sec[t], n*Tan[t]} *)

Let's use the sketch from wikipedia and name the points in the same way:

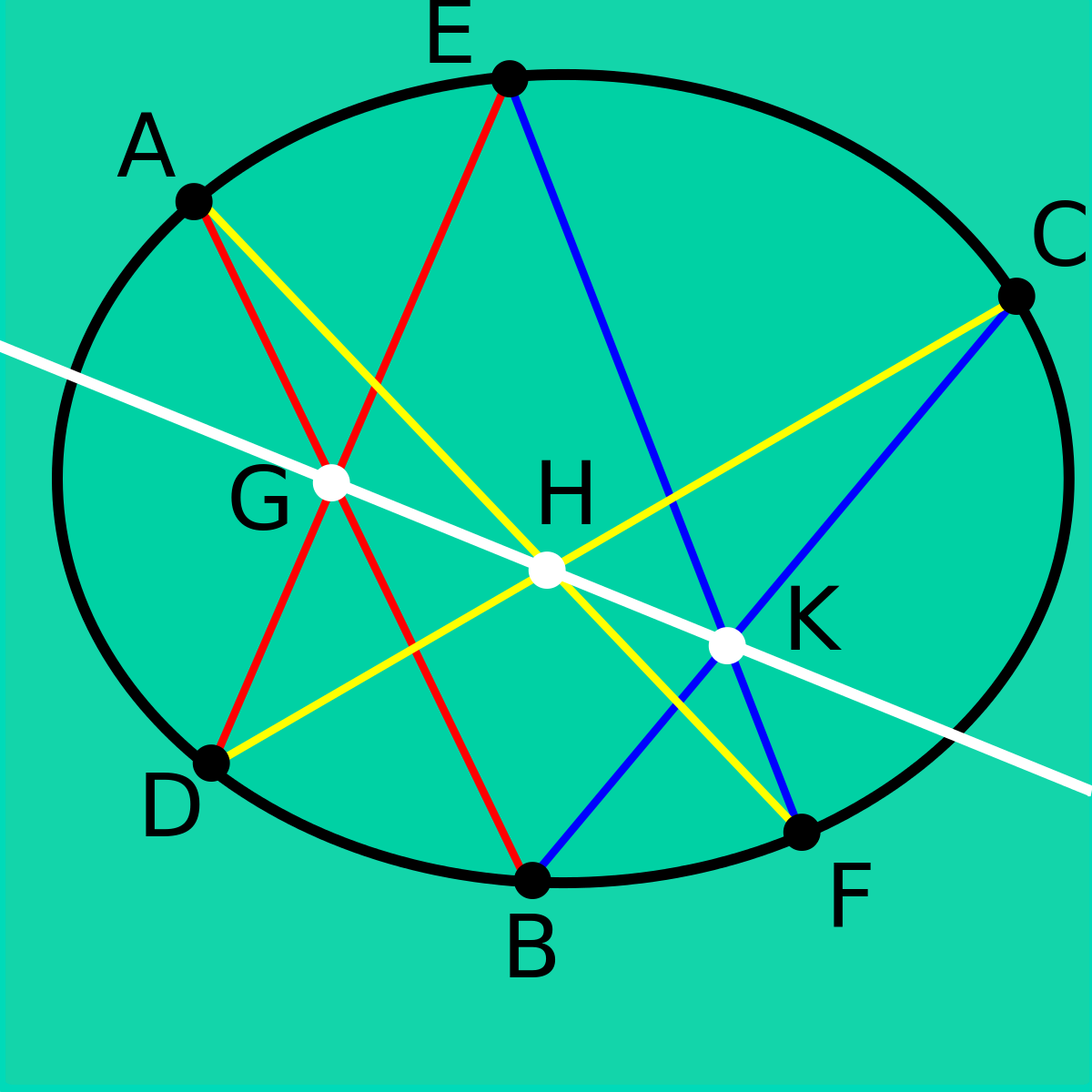
g = segmentIntersection[pt[a], pt[f], pt[c], pt[d]][[3]];
h = segmentIntersection[pt[a], pt[b], pt[d], pt[e]][[3]];
k = segmentIntersection[pt[b], pt[c], pt[e], pt[f]][[3]];

Check if $GHK$ are collinear by the following code and syntax sugar of Cross. The idea is $GHK$ is collinear if and only if the normal vector $V$ of $GH$ is perpendicular to $HK$ ( $V \cdot HK = 0$ )

AbsoluteTiming[Framed[Cross[g - h].(h - k) // Simplify]]
(*{ 0.93, 0 }*)

The code above returns $0$ in less than $1$ sec. Hence it completes the proof. If you use pt2[t] for hyperbola, the result is the same.

Remark

This algebraic method is very generic (except the case with parallel opposite sides) and covers all 60 cases of hexagon given 6 fixed points (generated by $(6-1)!/2 = 60$, which is all circular permutation of the indices and halved by reflection symmetry e.g. 1-2-3-4-5-6 = 2-3-4-5-6-1 = 1-6-5-4-3-2)