@Gianluca Gorni : Nice - simple, but very intuitive!

I guess for the full solution one needs ParametricNDSolve and friends:

ClearAll["Global`*"]
(* define the Lotka model: *)
x0 = 2; y0 = 1.5;
tRange = {t, 0, 30};
deq = {x'[t] == x[t] (1 - y[t]), y'[t] == y[t] (-\[Lambda] + x[t]), x[0] == x0, y[0] == y0};
(* solve it: *)
lotka = ParametricNDSolveValue[deq, {x[t], y[t]}, tRange, {\[Lambda]}];
(* show the solution: *)
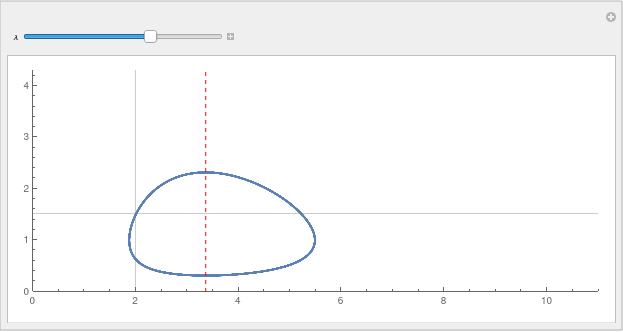
Manipulate[ParametricPlot[lotka[\[Lambda]], Evaluate@tRange, PlotRange -> {{0, 11}, {0, 4.3}}, PerformanceGoal -> "Quality", 
  ImageSize -> Large, GridLines -> {{x0}, {y0}}, Epilog -> {Dashed, Red, 
    InfiniteLine[{{\[Lambda], 0}, {\[Lambda], 1}}]}], {\[Lambda], .3, 5}]

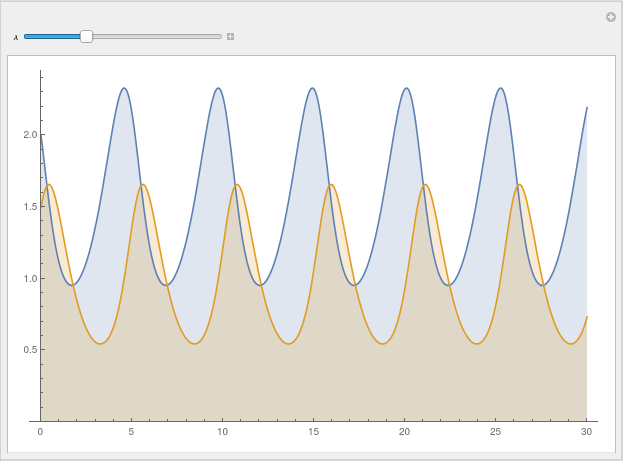
Manipulate[
 Plot[Evaluate@lotka[\[Lambda]], tRange, Filling -> Bottom, 
  PlotRange -> {0, Automatic}, ImageSize -> Large], {\[Lambda], 0, 5}]

Yeah I know but I have to do it. Thank you i just try your code! Now the most important for my document it's the diagram with (x+y) in function of time. The graph under on the website cnrs.

Have you an idea or something to help me on that? Sorry I don't want to take your time if you can't it's okay ;)