Message Boards Message Boards

Why Wolfram|Alpha gives the right result?

!Arc length integral][1]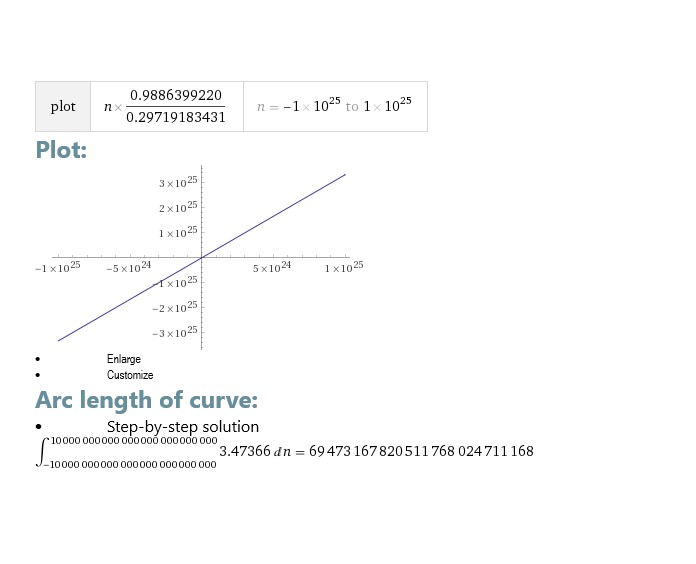Arc length integral with the right value

I would like to know why I can not get the value for the arc integral using Mathematica 12.0 , the value of 69473167820511768024711168 has all the digits different from each other while the value I get using

n=100000000000 a= 0.988639922/0.29719183431 b=Sqrt[a^2+1] c=nb2 n=N[c]

just returns me 6.94732*10^11 instead of all the digits that are supposed to exist for the right calculus of the arc integral, which is necessary for me to prove that it is a non trivial zero, Wolfram|Alpha gives me the correct value while I can not get it by writing lines of a program on Mathematica, could anyone help me I have just proven that the formula below gives non trivial zeros numbers that are very closely related to prime finding, which can be done using Wolfram|Alpha but I can not reproduce it on my computer.

Could anyone help me to reproduce what Wolfram|Alpha does?
POSTED BY: Luis Felipe Massena Misiec
8 Replies
Sort By:

Have you tried DecimalForm[c]?
POSTED BY: Gianluca Gorni

Yes I tried, using the Microsoft calculator it gives decimal places that seems endless and they seem to be extremely important for the result.
POSTED BY: Luis Felipe Massena Misiec

I have used DecimalForm and NumberForm, but the results of the calculation keeps me giving the square root of the numbers without giving me the result in numbers it gives me the drawing of the root with the number inside.

n=10000000000000000
a= 0.988639922/0.29719183431
NumberForm[N[a],40]
a1=NumberForm[a]
b=Sqrt[1+a1^2]
N[b]
bb=NumberForm[N[b],40]
b1=DecimalForm[bb]
c=n*b1*2
n=N[c,30]
DecimalForm[c]

`
POSTED BY: Luis Felipe Massena Misiec

The control N[a] that should give any numerical precision is not working. it gives the partial result of the numbers when elevated to any number it gives me the number raised to that number, but not the number with precision....Am I being guarded for some security issue? I am dealing with a prime algorithm finder that is very very fast, but I need it to prove the correlation that I have already noticed using Wolfram|Alpha, that the arc integral of n*0.988639922/0.29719183431 gives me non trivial zeros of Riemann that are in some cases just 1 far from the primes. I really need some help here.
POSTED BY: Luis Felipe Massena Misiec

For instance: done with an unlimited decimal places calculator aplying the formula of arc length for the numbers sqrt(1+(0.988639922/0.29719183421)^2) multiplied by the number of digits in the decimal place=69473167820511765242830133883162231196373893172462572947321681009276855429531868770882474054742274999418781196191128350605290638907281085633288937673680524199820066895936872314770237447995716771439959238004273486653770489519884087184561255933086729316005893883052796589968722075656357507968378869005241089165689837538775946470654446499501966076614890157622775988094202464078929288907735084091176712819439586018201262584675330599303231799651328074634544385044419476755076985251636084219268328080088251662043698866454523084731639802544765817015037852583580045461950139773968906062830312323507628556726568436388771648582054725350555439952871014106950029398605002226628662285437033779318551536747294374952255496472680780665826457366896250220249866954099419856397786258180576705276869616498812031948075619511682529816958383878485379938346995226313984712037892411186524390370830098196489452622389323720195586168765517245297601070346396828054779915463530671108671936053175605957994436181065402719501539164 ( non trivial zero)

which is close to :

69473167820511765242830133883162231196373893172462572947321681009276855429531868770882474054742274999418781196191128350605290638907281085633288937673680524199820066895936872314770237447995716771439959238004273486653770489519884087184561255933086729316005893883052796589968722075656357507968378869005241089165689837538775946470654446499501966076614890157622775988094202464078929288907735084091176712819439586018201262584675330599303231799651328074634544385044419476755076985251636084219268328080088251662043698866454523084731639802544765817015037852583580045461950139773968906062830312323507628556726568436388771648582054725350555439952871014106950029398605002226628662285437033779318551536747294374952255496472680780665826457366896250220249866954099419856397786258180576705276869616498812031948075619511682529816958383878485379938346995226313984712037892411186524390370830098196489452622389323720195586168765517245297601070346396828054779915463530671108671936053175605957994436181065402719501539141 ( Prime number ) checked with PrimeQ of wolfram mathematica.

but i can not get this value out of wolfram mathematica!!! Please help P.S: If you are curious to know how i got those numbers please visit " Finding primes and nontivial zeros" at figshare.com under my name Luis Felipe Massena Misiec
POSTED BY: Luis Felipe Massena Misiec

The whole number did not appear. It has 2000 digits.
POSTED BY: Luis Felipe Massena Misiec

If you use machine numbers in the input, then N will not magically make them have higher precision. So the suggestion would be to work with exact numbers. Anything else is just in effect making up digits.
POSTED BY: Daniel Lichtblau

Thank you very much Mr.Daniel, but if I simply use Wolfram as a calculator to make 0.988639922/0.29719183431 it does not show the decimal places that seem to be infinity for this calculation, I have used unlimited calculators on the web and it shows me more than 2000 digits for the decimal places I wonder why...
POSTED BY: Luis Felipe Massena Misiec
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract