Group Abstract Group Abstract

Message Boards Message Boards

How to use TransformedRegion

Starting with a polygon from the countries data set, I am interested in building a 3D extrusion of that country polygon to assemble it in 3D with the other countries.

I get the polygon and extrude it using regions:

 data = Entity["Country", "UnitedStates"]["Polygon"][[1, 1, 1]];
R = BoundaryMeshRegion[data, Line[Join[Range[Length[data]], {1}]] ];
R3 = RegionProduct[R, MeshRegion[{{0}, {1}}, Line[{1, 2}]]]

It looks like this: as expected

a flat extruded version of the USA mainland

Now I would like to map it to earth, a sphere, and change the coordinates from Lat,Long, Altitude to {x,y,z}

TransformedRegion[R3, (1 + 
     Indexed[#, 3]/10) {Cos[Indexed[#, 2] N[Degree]]*
     Cos[Indexed[#, 1] N[Degree]], Sin[Indexed[#, 1] N[Degree]], 
    Sin[Indexed[#, 2] N[Degree]]*Cos[Indexed[#, 1] N[Degree]]} &]

But I only get

enter image description here

What am I missing?

Thank you,

Luc

POSTED BY: Luc Barthelet
5 Replies
Sort By:

Thank you Steffen, I will investigate asap.
POSTED BY: Luc Barthelet

Your problem is mainly twofold:

a) the transform given to TransformedRegion is just working with

(1 + Indexed[#, 3]/10) {Cos[Indexed[#, 2] N[Degree]]*
     Cos[Indexed[#, 1] N[Degree]], Sin[Indexed[#, 1] N[Degree]], 
    Sin[Indexed[#, 2] N[Degree]]*Cos[Indexed[#, 1] N[Degree]]} & /@ R3

b) Region is a difficult built-in. The region created that way does not work with any of the given examples in the documentation for TransformedRegion. The problem gets simpler for the entity itself.

Mathematica has sometimes built-in serving the same purpose with an only slight difference in the output.

So TransformedRegion might be impressive for newsy starting to operate on regions. But these are already 3D objects. Mathematica provides built-ins like 

> Rotate[R3, \[Pi], {0, 0, 1}]

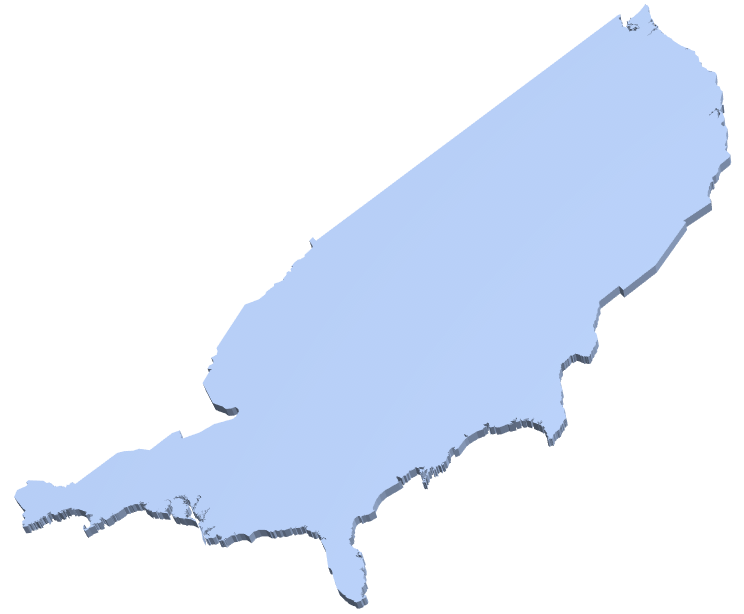
Graphics3D of the embossed country USA

A nice input to do the desired result is:

> NormalizeGraphics[g_] :=  
> Internal`InheritedBlock[{System`Private`InternalNormal},   
> Unprotect[System`Private`InternalNormal];  
> System`Private`InternalNormal[
>     gr : _Rotate | _Translate | _Scale | _GeometricTransformation, _] \ := Module[{tmp = Quiet[transform2D[gr], TransformedRegion::reg]}, 
>     tmp /; Head[tmp] =!= TransformedRegion];   Normal[g, {Rotate, Scale, Translate, GeometricTransformation}]]
>

NormalizeGraphics@R3

Graphics3D output of NormalizeGraphics@R3

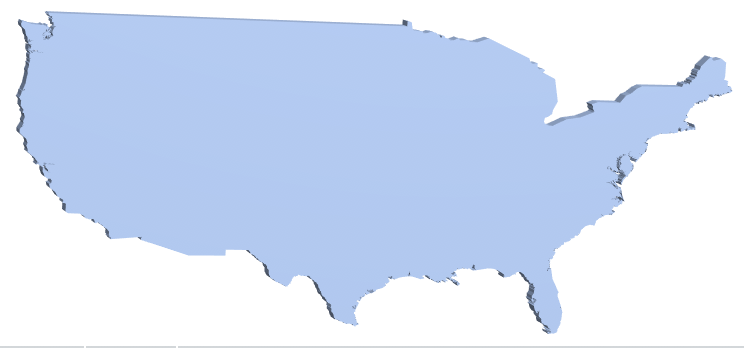
This is an input already published in Why doesn't normal work on Geometrictransformation on mathematica.stackexchange.com in August 2017.

I hope that helps or already answers the problem.
POSTED BY: Steffen G. Jaeschke
Updating Name
Updating Name
Posted 5 years ago

Henrik,

I always thought Alaska were part of the United States

You have to use GeoVariant if you want to include Alaska, Hawaii and other US territories.
POSTED BY: Updating Name

Hello ...(?),

Many thanks for this useful hint!

Regards -- Henrik
POSTED BY: Henrik Schachner

Hello Luc,

I do not know what the problem might be using TransformedRegion. My proposal is simply doing it "by hand" like so (assuming the globe is a perfect sphere and using replacement rules to make it independent of nesting depth):

(* getting the data: *)
poly = Entity["Country", "UnitedStates"]["Polygon"];
(* converting GeoPositions into spherical angles: *)
coords = poly[[1, 1]] \[Degree] /. {\[Theta]_, \[Phi]_} :> {Pi/2 - \[Theta], \[Phi]};
r2 = DiscretizeRegion@Polygon[coords];
(* adding 3rd dimension: *)
r3 = RegionProduct[Line[{{0.98}, {1.02}}], r2];
(* disassembling into primitives: *)
prisms = MeshPrimitives[r3, 3];
(* points of primitives are now in sperical coordinates => 
replace with Cartesian coordinates: *)
prismsXYZ = prisms /. {r_, \[Theta]_, \[Phi]_} :> FromSphericalCoordinates[{r, \[Theta], \[Phi]}];
Graphics3D[prismsXYZ, ImageSize -> Large]

enter image description here

Up to now I have no idea about converting this back into a Region - but maybe that does help nevertheless. Regards -- Henrik

(I always thought Alaska were part of the United States ...)

POSTED BY: Henrik Schachner
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard