I would like to write equations in the form as following: 1/2y + 3/8 x == 2/5 z + w
When this is evaluated it returns 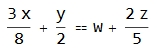
however I would like keep the product terms separated from the symbols and the order of addition as placed in the original equation i.e. I would like to keep the following format:
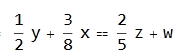
My solution so far is to use this syntax:
HoldForm[HoldForm[1/2]*y + HoldForm[3/8]*x] ==
HoldForm[HoldForm[2/5] *z + w]
but I am not aware how I can generalize this in a programatic way or if there is any other more simple way to achive the same result.
Any suggestion is welcome.