Message Boards Message Boards

0
|
4942 Views
|
5 Replies
|
1 Total Likes
View groups...
Share
Share this post:

Separating product terms and keep a custom order in addition

I would like to write equations in the form as following: 1/2y + 3/8 x == 2/5 z + w

When this is evaluated it returns 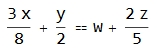enter image description here

however I would like keep the product terms separated from the symbols and the order of addition as placed in the original equation i.e. I would like to keep the following format:

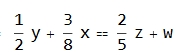
enter image description here

My solution so far is to use this syntax:

HoldForm[HoldForm[1/2]*y + HoldForm[3/8]*x] == 
 HoldForm[HoldForm[2/5] *z + w]

but I am not aware how I can generalize this in a programatic way or if there is any other more simple way to achive the same result.

Any suggestion is welcome.
POSTED BY: Artin Hatzikioseyian
5 Replies
Sort By:

You can try with a pattern replacement. For example

(1/2 y + 3/8 x == 2/5 z + w) /.
 coeff_?NumberQ*v__Symbol :>
  Inactive[Times][coeff, v]
POSTED BY: Gianluca Gorni

Thank you for your reply. This really works with the multiplication term, but how can I keep also the order of addition.
POSTED BY: Artin Hatzikioseyian

I think for the addition order I cannot avoid the hard way:

ClearAttributes[Plus, Orderless]

while for the product terms:

Replace[expression, Times[x_, y_] -> HoldForm[HoldForm[x]*y], Infinity]
POSTED BY: Artin Hatzikioseyian

Modifying the function Plus sounds dangerous. I would rather make it Inactive:

(Inactive[Plus][1/2 y, 3/8 x] == Inactive[Plus][2/5 z, w]) /. 
 coeff_?NumberQ*v__Symbol :> Inactive[Times][coeff, v]
POSTED BY: Gianluca Gorni

Thank you for your comments and help.
POSTED BY: Artin Hatzikioseyian
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract