The most updated version of the code is present on: https://github.com/alihashmiii/2D-vertex-model
The introduction to what vertex models are, is given in an earlier post: https://community.wolfram.com/groups/-/m/t/2051277
Below is a simpler two-dimensional vertex model implemented in version 12.1 to minimize an energy function defined on a polygonal mesh (e.g. to simulate how cell shapes and curvature evolve in biological tissues).
Geometrical functions
Clear[getCounterClockwise];
getCounterClockwise[vertex_, vertices_] := Block[{pos, v},
pos = First @@ Position[vertices, vertex];
If[pos == Length[vertices], pos = 1, pos += 1];
vertices[[pos]]
];
Clear[getClockwise];
getClockwise[vertex_, vertices_] := Block[{ls, pos},
pos = First @@ Position[vertices, vertex];
If[pos == 1, pos = Length[vertices], pos -= 1];
vertices[[pos]]
];
Clear[areaOfPolygon];
areaOfPolygon[cells_ /; Head[cells] === Association] := Map[Area@*Polygon, cells];
Clear[areaPolygon];
areaPolygon[vertices_] := Block[{edges},
edges = Partition[vertices, 2, 1, 1];
0.5 Abs@Total[(#[[1, 1]]*#[[2, 2]]) - (#[[2, 1]]*#[[1, 2]]) & /@ edges]
];
Clear[perimeterOfPolygon];
perimeterOfPolygon[cells_/; Head[cells] === Association] := (Perimeter@*Polygon)/@cells;
Clear[perimeterPolygon];
perimeterPolygon[vertices_] := Block[{edges},
edges = Partition[vertices, 2, 1, 1];
Total[Apply[EuclideanDistance] /@ edges]
];
Clear[centroidPolygon];
centroidPolygon[vertices_] := Mean@vertices;
Clear[polyCounterClockwiseQ];
polyCounterClockwiseQ[poly_] :=
Block[{area = 0, j, vertLength = Length[poly]},
Do[
j = Mod[i, vertLength] + 1;
area += poly[[i, 1]]*poly[[j, 2]];
area -= poly[[j, 1]]*poly[[i, 2]],
{i, vertLength}];
(area/2) > 0
];
Clear[sortPointsCC];
sortPointsCC[polyinds_, indTopts_, ptsToInds_] :=
Block[{cent, ordering, polyPoints},
polyPoints = Lookup[indTopts, polyinds];
cent = Mean@polyPoints;
ordering =
Ordering[ArcTan[#[[1]], #[[2]]] &@(# - cent) & /@ polyPoints];
Lookup[ptsToInds, Part[polyPoints, ordering]]
];
Mesh Restructuring operations
T1 transition (neighbour switching)
Clear@edgesforT1;
edgesforT1[edgeLs_, indToPts_, threshLength_ : 0.0015] :=
Block[{edges, dist},
edges = Lookup[indToPts, #] & /@ edgeLs;
dist = EuclideanDistance @@ # & /@ edges;
{Pick[edges, Thread[dist <= threshLength], True],
Pick[edgeLs, Thread[dist <= threshLength], True]}
];
Clear@T1transitionFn;
T1transitionFn[edges_, indToPtsAssoc_, vertexToCellG_, cellToVertexG_, dSep_ : 0.01] :=
Block[{findEdges, edgeind, connectedcellKeys, edge, newpts, cellvertIndices,
cellvertices, pos, cellpolys, memF, keyscellP, selcellKeys, ptToCell, newptsindices,
indToPts = indToPtsAssoc, ptsToInds, PtIndToCell, keysToMap, cellindicesAssoc, f1,
otherkeys, f2, polysharingEdge, bag = CreateDataStructure["DynamicArray"],
vertToCellG = vertexToCellG, cellToVertG = cellToVertexG, testpts, edgechanged},
{edgechanged, findEdges} = edgesforT1[edges, indToPts];
(* finding all possible edges for T1 transition *)
If[findEdges != {},
Scan[
(edgeind = #;
If[ContainsAll[Keys[indToPts], edgeind],
(* should be an edge not connected to an edge that has already undergone a T1 *)
connectedcellKeys =
DeleteDuplicates[Flatten@Lookup[vertToCellG, edgeind]];
cellvertIndices = Lookup[cellToVertG, connectedcellKeys];
edge = Lookup[indToPts, edgeind];
newpts = With[{midPt = Mean[edge]},
midPt + dSep Normalize[(# - midPt)] & /@Flatten[RotationTransform[-(\[Pi]/2), midPt] /@ {edge}, 1]
];
testpts = With[{midPt = Mean[edge]},
midPt + 0.000001 Normalize[(# - midPt)] & /@ newpts
];
pos = Position[cellvertIndices, {OrderlessPatternSequence[___,
First@edgeind, ___, Last@edgeind, ___]}, {1}];
polysharingEdge = Extract[cellvertIndices, pos];
(* the edge should not be part of any \[CapitalDelta] *)
If[(AllTrue[polysharingEdge, Length[#] != 3 &]) &&
ContainsNone[edgeind, Union@*Flatten@*Normal@bag],
cellvertices = Map[Lookup[indToPts, #] &, cellvertIndices];
cellpolys = Polygon /@ cellvertices;
memF = Function[x, RegionMember@x, Listable][Extract[cellpolys, pos]];
If[k == 17, Print["conn cells:", connectedcellKeys]];
keyscellP = Extract[connectedcellKeys, pos];
selcellKeys = Thread[keyscellP -> memF];
ptToCell = Quiet[# -> First@@Select[selcellKeys, Function[x, Last[x][#]]] & /@
testpts /. HoldPattern[_ -> First[]] -> Nothing] ;(*pt to cell *)
ptToCell = ptToCell /. Thread[testpts -> newpts];
newptsindices = Range[# + 1, # + 2] &[Max[Keys@indToPts]];
KeyDropFrom[indToPts, edgeind];
AppendTo[indToPts, Thread[newptsindices -> newpts]];
ptsToInds = AssociationMap[Reverse, indToPts];
bag["Append", edgeind];
PtIndToCell = MapAt[ptsToInds, ptToCell, {All, 1}] /. Rule -> List ;(*index to cell*)
keysToMap = MapAt[Key, PtIndToCell, {All, 2}];
cellindicesAssoc = AssociationThread[connectedcellKeys, cellvertIndices];
f1 =
Fold[MapAt[
Function[x,
DeleteDuplicates[
x /. Thread[ edgeind -> #2[[1]] ]]], #1, #2[[2]]] &,
cellindicesAssoc, keysToMap];
otherkeys = List@*Key /@ Complement[connectedcellKeys, keyscellP];
f2 =
MapAt[(# /. (Alternatives @@ edgeind) ->
Splice[newptsindices] //
sortPointsCC[#, indToPts, ptsToInds] &) &, f1,
otherkeys];
AppendTo[cellToVertG, f2];
vertToCellG = GroupBy[Flatten[(Reverse[#, 2] &)@*Thread /@Normal@cellToVertG], First -> Last];
]
]) &,
findEdges]
];
{edgechanged, indToPts, cellToVertG, vertToCellG}
];
T2 transitions (cell removal)
Clear@cellsforT2;
cellsforT2[areaAssoc_, cellVertexG_, thresh_ : 10^-5] :=
Block[{keys, ls, inds},
keys = Keys@Select[areaAssoc, # < thresh &];
ls = Lookup[cellVertexG, keys];
inds = Flatten@Position[ls, x_ /; (3 <= Length[x] <= 6), {1}];
If[inds != {}, {keys[[inds]], ls[[inds]]}, {{}, {}}] (*cell inds, vertices*)
];
Clear@T2TransitionFn;
T2TransitionFn[{cellsToRemove_, vertindsRemove_}, indTopts_,
cellToVertexG_, areaPolygonAssoc_, periPolygonAssoc_] :=
Block[{newVertices, maxkey, newindices,
newentries, indToPts = indTopts, ruleDisp, removeentries,
CVG = cellToVertexG, notaCell, VertCellGrouping},
newVertices = Mean@Lookup[indTopts, #] & /@ vertindsRemove;
maxkey = Max@*Keys@indTopts;
newindices = Range[maxkey + 1, maxkey + Length[newVertices]];
newentries = Thread[newindices -> newVertices];
KeyDropFrom[indToPts, Union@Flatten[vertindsRemove]];
AppendTo[indToPts, newentries];
ruleDisp =
Dispatch@
Flatten[MapThread[
Thread[#1 -> #2] &, {vertindsRemove, newindices}]];
removeentries = Union@Flatten@cellsToRemove;
KeyDropFrom[CVG, removeentries];
CVG = DeleteDuplicates /@ Replace[CVG, ruleDisp, {2}];
notaCell = Keys@Select[Length /@ CVG, # < 3 &];
KeyDropFrom[CVG, notaCell];
VertCellGrouping =
GroupBy[Flatten[(Reverse[#, 2] &)@*Thread /@ Normal@CVG],
First -> Last];
{indToPts, CVG, VertCellGrouping,
KeyDrop[areaPolygonAssoc, removeentries~Join~notaCell],
KeyDrop[periPolygonAssoc, removeentries~Join~notaCell]}
] /; vertindsRemove != {};
Cell Divisions
probability of cell division is based on the cell area
Clear[selectDivCells];
selectDivCells[areaPolygon_, areathresh_ : 2.2, thresh_ : 0.0025] :=
Block[{candidates, pos},
candidates =
Normal@Select[areaPolygon/Mean[areaPolygon], # > areathresh &];
pos = Position[0.1 RandomReal[1, Length@candidates],
x_ /; x < thresh];
Keys@Extract[candidates, pos]
];
Clear[cellDivision];
cellDivision[polygonind_, indToPoints_, areaAssoc_, perimAssoc_,
cellToVertG_] :=
Block[{x, y, num, matrix, xx, xy, yy, eigvals, eigVecs, maxeigpos,
cent, edges, edgesL, intersects, intersectionPts,
posIntersections, repPart, \[Alpha], \[Beta], polygonPts,
newkeys = Range[# + 1, # + 2] &[Max@Keys[indToPoints]],
newPtToInds, indtoPtAssoc = indToPoints, ptToIndAssoc, edgeinds,
contour, poly1, poly2, res, seq,
newcells = Range[# + 1, # + 2] &[Max@Keys[areaAssoc]],
CVG = cellToVertG, addcellsRule, polygonPtsInds, VCG},
VCG = GroupBy[Flatten[(Reverse[#, 2] &)@*Thread /@ Normal@CVG],
First -> Last];
polygonPtsInds = CVG[polygonind];
num = Length@polygonPtsInds;
ptToIndAssoc = AssociationMap[Reverse, indToPoints];
polygonPts = Lookup[indToPoints, polygonPtsInds];
Evaluate[Table[{Subscript[x, i], Subscript[y, i]}, {i, num}]] =
polygonPts;
Subscript[I, xx] = (1/12) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(num - 1\)]\(\((
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(y\), \(i + 1\)]\ -
\*SubscriptBox[\(x\), \(i + 1\)]
\*SubscriptBox[\(y\), \(i\)]\ )\) \((
\*SuperscriptBox[
SubscriptBox[\(y\), \(i\)], \(2\)] +
\*SubscriptBox[\(y\), \(i\)]
\*SubscriptBox[\(y\), \(i + 1\)] +
\*SuperscriptBox[
SubscriptBox[\(y\), \(i + 1\)], \(2\)])\)\)\);
Subscript[I, yy] = (1/12) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(num - 1\)]\(\((
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(y\), \(i + 1\)]\ -
\*SubscriptBox[\(x\), \(i + 1\)]
\*SubscriptBox[\(y\), \(i\)]\ )\) \((
\*SuperscriptBox[
SubscriptBox[\(x\), \(i\)], \(2\)] +
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(x\), \(i + 1\)] +
\*SuperscriptBox[
SubscriptBox[\(x\), \(i + 1\)], \(2\)])\)\)\);
Subscript[I, xy] = (1 /24) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(num - 1\)]\(\((
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(y\), \(i + 1\)]\ -
\*SubscriptBox[\(x\), \(i + 1\)]
\*SubscriptBox[\(y\), \(i\)]\ )\) \((
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(y\), \(i + 1\)] + 2
\*SubscriptBox[\(x\), \(i\)]
\*SubscriptBox[\(y\), \(i\)] + 2
\*SubscriptBox[\(x\), \(i + 1\)]
\*SubscriptBox[\(y\), \(i + 1\)] +
\*SubscriptBox[\(x\), \(i + 1\)]
\*SubscriptBox[\(y\), \(i\)])\)\)\);
Table[{Unevaluated[Subscript[x, j]] =.,
Unevaluated[Subscript[y, j]] =.}, {j, num}];
matrix = ( {
{Subscript[I, xx], -Subscript[I, xy]},
{-Subscript[I, xy], Subscript[I, yy]}
} );
{eigvals, eigVecs} = Eigensystem@matrix;
maxeigpos = Position[eigvals, Max@eigvals];
{edges, edgeinds} =
Partition[#, 2, 1, 1] & /@ {polygonPts, polygonPtsInds};
edgesL = Line /@ edges;
cent = centroidPolygon[polygonPts];
intersects =
RegionIntersection[
InfiniteLine[{cent,
cent + Extract[eigVecs, maxeigpos][[1]]}], #] & /@ edgesL;
intersectionPts = Cases[intersects, {(_Real | _Integer) ..}, {3}];
newPtToInds = Thread[intersectionPts -> newkeys];
posIntersections = Flatten@Position[intersects, _Point, {1}];
MapThread[
(res = Complement[Intersection @@ Lookup[VCG, #2], {polygonind}];
If[res != {},
seq = Partition[CVG[First@res], 2, 1, 1];
AppendTo[CVG,
First@res ->
DeleteDuplicates@
Flatten@SequenceSplit[
seq, {x___,
p : {OrderlessPatternSequence[#2[[1]], #2[[-1]]]},
y___} :> {x, Insert[p, #1, 2], y}]
];
]) & , {newkeys, edgeinds[[posIntersections]]}];
repPart =
Thread[{Thread[{ReverseSort@posIntersections, 2}],
Reverse[intersectionPts]}];
{\[Alpha], \[Beta]} = intersectionPts;
AppendTo[ptToIndAssoc, newPtToInds];
AppendTo[indtoPtAssoc, Reverse[newPtToInds, 2]];
contour =
DeleteDuplicates@
Flatten[Fold[Insert[#1, #2[[2]], #2[[1]]] &, edges, repPart], 1];
poly1 =
Join @@ SequenceCases[contour, {___, \[Alpha]} | {\[Beta], ___}];
poly2 = Join @@ SequenceCases[contour, {\[Alpha], __, \[Beta]}];
KeyDropFrom[CVG, polygonind];
addcellsRule = Thread[newcells -> {poly1, poly2}];
AppendTo[CVG, addcellsRule /. ptToIndAssoc];
{indtoPtAssoc, CVG,
Append[KeyDrop[areaAssoc, polygonind],
MapAt[Area@*Polygon, addcellsRule, {All, 2}]],
Append[KeyDrop[perimAssoc, polygonind],
MapAt[Perimeter@*Polygon, addcellsRule, {All, 2}]]}
];
Compute Forces
Subscript[F, AreaElasticity][indTopts_, vertexToCellG_,
cellToVertexG_, areaPolygonAssoc_] :=
Block[{cellinds, temp, vertKeys = Keys[indTopts],
vertLs, vertex, gc, gcc, diffVec, grad, coeff},
First@*Last@Reap@Do[
cellinds = Lookup[vertexToCellG, i];
temp = {0, 0};
vertex = indTopts[i];
Do[
vertLs = Lookup[indTopts, Lookup[cellToVertexG, j]];
gcc = getCounterClockwise[vertex, vertLs];
gc = getClockwise[vertex, vertLs];
diffVec = gcc - gc;
grad = 0.5*{{0, 1}, {-1, 0}}.diffVec;
coeff = ka (areaPolygonAssoc[j] - A0);
temp += grad*coeff, {j, cellinds}
];
Sow@temp, {i, vertKeys}]
];
Subscript[F, PerimeterElasticity][indTopts_, vertexToCellG_,
cellToVertexG_, periPolygonAssoc_] :=
Block[{cellinds, temp, vertKeys = Keys[indTopts], vertLs,
vertex, gc, gcc, v1, v2, coeff, grad},
First@*Last@Reap@Do[
cellinds = Lookup[vertexToCellG, i];
temp = {0, 0};
vertex = indTopts[i];
Do[
vertLs = Lookup[indTopts, Lookup[cellToVertexG, j]];
gc = getClockwise[vertex, vertLs];
gcc = getCounterClockwise[vertex, vertLs];
v1 = Normalize[vertex - gc];
v2 = Normalize[vertex - gcc];
grad = v1 + v2;
coeff = \[Gamma] (periPolygonAssoc[j] - P0);
temp += grad*coeff, {j, cellinds}];
Sow@temp, {i, vertKeys}]
];
Subscript[F, LineTension][indTopts_, vertexToCellG_, cellToVertexG_] :=
Block[{cellinds, temp, vertKeys = Keys@indTopts, vertLs,
vertex, gc, gcc, v1, v2},
First@*Last@Reap@Do[
cellinds = Lookup[vertexToCellG, i];
temp = {0, 0};
vertex = indTopts[i];
Do[
vertLs = Lookup[indTopts, Lookup[cellToVertexG, j]];
gc = getClockwise[vertex, vertLs];
gcc = getCounterClockwise[vertex, vertLs];
v1 = Normalize[vertex - gc];
v2 = Normalize[vertex - gcc];
temp += \[Kappa] v1 + \[Kappa] v2, {j, cellinds}];
Sow@temp, {i, vertKeys}]
];
Subscript[F, ActiveContraction][indTopts_, vertexToCellG_,
cellToVertexG_, areaPolygonAssoc_] :=
Block[{cellinds, temp, vertKeys = Keys@indTopts, vertLs,
vertex, gc, gcc, diffVec, grad, coeff},
First@*Last@Reap@Do[
cellinds = Lookup[vertexToCellG, i];
temp = {0, 0};
vertex = indTopts[i];
Do[
vertLs = Lookup[indTopts, Lookup[cellToVertexG, j]];
gcc = getCounterClockwise[vertex, vertLs];
gc = getClockwise[vertex, vertLs];
diffVec = gcc - gc;
grad = 0.5*{{0, 1}, {-1, 0}}.diffVec;
coeff = 0.1 ka *(areaPolygonAssoc[j]);
temp += grad*coeff, {j, cellinds}];
Sow@temp, {i, vertKeys}]
];
Subscript[F, T][indTopts_, vertexToCellG_, cellToVertexG_,
areaPolygonAssoc_, periPolygonAssoc_] := -(
Subscript[F, AreaElasticity][indTopts, vertexToCellG,
cellToVertexG, areaPolygonAssoc] +
Subscript[F, PerimeterElasticity][indTopts, vertexToCellG,
cellToVertexG, periPolygonAssoc] +
Subscript[F, LineTension][indTopts, vertexToCellG,
cellToVertexG] +
Subscript[F, ActiveContraction][indTopts, vertexToCellG,
cellToVertexG, areaPolygonAssoc]
);
Initialize parameters, create mesh and run simulation
ka = 1; A0 = 1; \[Gamma] = 0.04*ka*A0; \[Delta]t = 0.02; P0 = 0; \[Kappa] = 0.025;
SeedRandom[3];
mesh = VoronoiMesh[RandomReal[1, {200, 2}], {{0, 1}, {0, 1}},
ImageSize -> Medium];
pts = MeshPrimitives[mesh, 0] /. Point -> Sequence;
cornerpts = pts[[-4 ;;]];
pts = pts[[1 ;; -5]];
$ptsToInd = ptsToInd = AssociationThread[pts -> Range@Length@pts];
$indTopts = indTopts = AssociationMap[Reverse][ptsToInd];
cellmeshprim = MeshPrimitives[mesh, 2];
cells = (MeshPrimitives[#, 0] & /@ cellmeshprim) /.
Point -> Sequence /. Thread[cornerpts -> Nothing];
$cellToVertexG =
cellToVertexG =
AssociationThread[Range[Length@cells] -> Map[ptsToInd, cells, {2}]];
$vertexToCell =
vertexToCell =
GroupBy[Flatten[(Reverse[#, 2] &)@*Thread /@ Normal@cellToVertexG],
First -> Last];
Lets see the initial mesh
Graphics[Map[{RandomColor[], Polygon@Lookup[indTopts, #]} &,
Values@cellToVertexG], ImageSize -> Medium]

$cellToPts = cellToPts = Lookup[indTopts, #] & /@ cellToVertexG;
$periPolygonAssoc = periPolygonAssoc = perimeterPolygon /@ cellToPts;
$areaPolygonAssoc = areaPolygonAssoc = areaPolygon /@ cellToPts;
pltOriginal = Graphics[{Black, Thick, Values@Map[Line[Join[##, {First@#}]] &@
Lookup[$indTopts, #] &, $cellToVertexG]}];

Running the simulation:
t = \[Delta]t;
indTopts = $indTopts;
ptsToInd = $ptsToInd;
vertexToCell = $vertexToCell;
cellToVertexG = $cellToVertexG;
periPolygonAssoc = $periPolygonAssoc;
areaPolygonAssoc = $areaPolygonAssoc;
cellToPts = $cellToPts;
edges = DeleteDuplicatesBy[
Flatten[Map[Partition[#, 2, 1, 1] &, Values@$cellToVertexG], 1],
Sort];
Module[{cellsToRemove, vertsToRemove, edgechanged, polydiv},
saveres = First@Last@Reap@Monitor[
While[t <= 80 \[Delta]t,
(* T2 transitions *)
{cellsToRemove, vertsToRemove} =
cellsforT2[areaPolygonAssoc, cellToVertexG];
If[cellsToRemove != {},
{indTopts, cellToVertexG, vertexToCell, areaPolygonAssoc,
periPolygonAssoc} =
T2TransitionFn[{cellsToRemove, vertsToRemove}, indTopts,
cellToVertexG, areaPolygonAssoc, periPolygonAssoc]
];
(* T1 transitions *)
edges =
DeleteDuplicatesBy[
Flatten[Map[Partition[#, 2, 1, 1] &, Values[cellToVertexG]],
1], Sort];
{edgechanged, indTopts, cellToVertexG, vertexToCell} =
T1transitionFn[edges, indTopts, vertexToCell, cellToVertexG];
cellToPts = Lookup[indTopts, #] & /@ cellToVertexG;
areaPolygonAssoc = areaPolygon /@ cellToPts;
periPolygonAssoc = perimeterPolygon /@ cellToPts;
(* Divisions *)
polydiv = selectDivCells[areaPolygonAssoc];
(*polydiv=pickcellsDiv[cellToVertexG,areaPolygonAssoc];*)
If[polydiv != {},
Scan[
({indTopts, cellToVertexG, areaPolygonAssoc,
periPolygonAssoc} =
cellDivision[#, indTopts, areaPolygonAssoc,
periPolygonAssoc, cellToVertexG]) &,
polydiv];
vertexToCell =
GroupBy[Flatten[(Reverse[#, 2] &)@*Thread /@
Normal@cellToVertexG], First -> Last];
];
(* update positions *)
indTopts =
AssociationThread[
Keys[indTopts] -> (Values[indTopts] +
Subscript[F, T][indTopts, vertexToCell, cellToVertexG,
areaPolygonAssoc, periPolygonAssoc] \[Delta]t)];
cellToPts = Lookup[indTopts, #] & /@ cellToVertexG;
areaPolygonAssoc = areaPolygon /@ cellToPts;
periPolygonAssoc = perimeterPolygon /@ cellToPts;
(*plt=Graphics[{ColorData[1][4],Thick,Values@Map[Line[
Join[##,{First@#}]]&@Lookup[indTopts,#]&,cellToVertexG]},
ImageSize\[Rule]Medium];*)
plt =
Graphics[{FaceForm[LightBlue], EdgeForm[Black],
Values[Polygon@Lookup[indTopts, #] & /@ cellToVertexG]}];
Sow[plt];
t += \[Delta]t;
], plt
]
];

the initial and and final geometry of the mesh are superimposed:
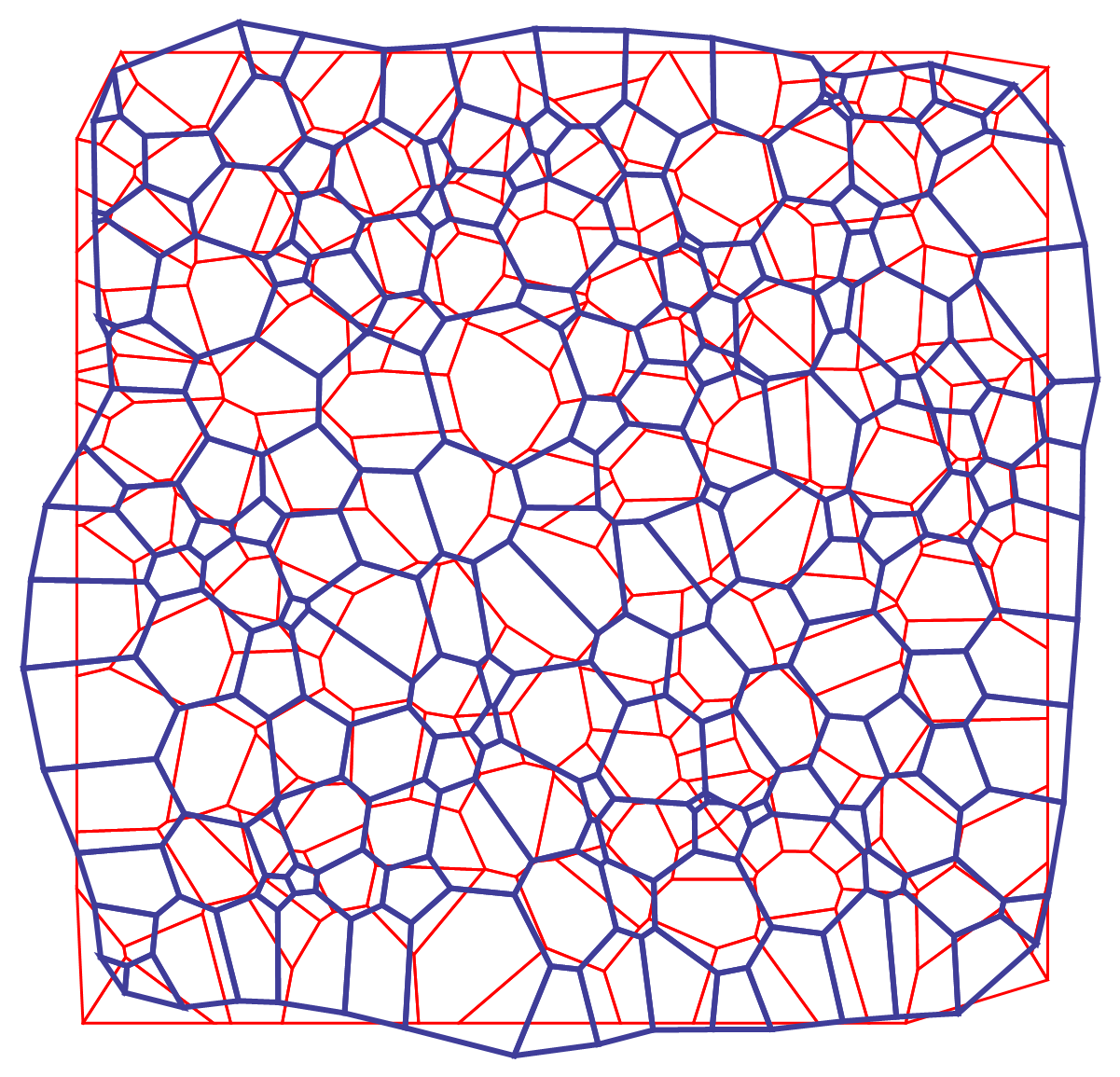
The notebook for non-periodic mesh is attached as a notebook below:
The code with periodic boundary condition is attached as a notebook below:
 Attachments:
Attachments: