Isn't the "classical" question usually, "For N people, what is the probability that
at least 2 share the same birthday?" I believe that is the solution to that is given by Marco. But, the original question seemed to be exactly two people out of 100. The "at least" probability would need to multiplied by the probability none of the other 98 share the same birthday as our lucky two.
So, let's try an approximation by brute force for exactly 2:
experiment := Max[Length /@ Gather[RandomInteger[{1, 365}, 100]]]
Histogram[Table[experiment, {10000}], {1}]
N@Count[Table[experiment, {100000}], 2]/100000
Playing with this a bit more: brute force probabilities that for n people, at most m share the same birthday:
exper[i_] := Max[Length /@ Gather[RandomInteger[{1, 365}, i]]]
probs = ParallelTable[((N@Count[Table[exper[#], {10000}], i]/10000) &) /@ Range[100], {i, 1, 10}]
ListPlot[probs, PlotRange -> All, Frame -> True,
AxesOrigin -> {0.5, 0.5},
FrameLabel -> {"Number of People", "Probability"},
PlotLegends -> Range[10]]
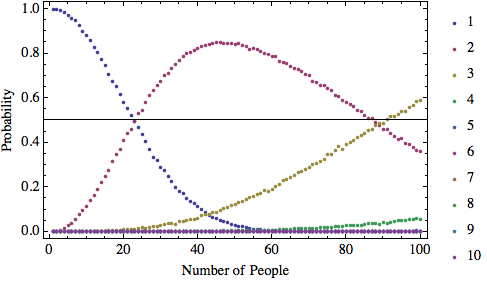
The crossings at p=1/2 are interesting.....