Thank you once again I have taken a look at it I just typed N[peaks] and N[zeros], thank you so much God bless you!!!

If anyone know how to get the values for x the abscissa where those points and peaks are, I would thank so much.

The code above does not evaluate correctly

Sum::itraw: Raw object 2 cannot be used as an iterator.

Sum::vloc: The variable 2 cannot be localized so that it can be assigned to numerical values.

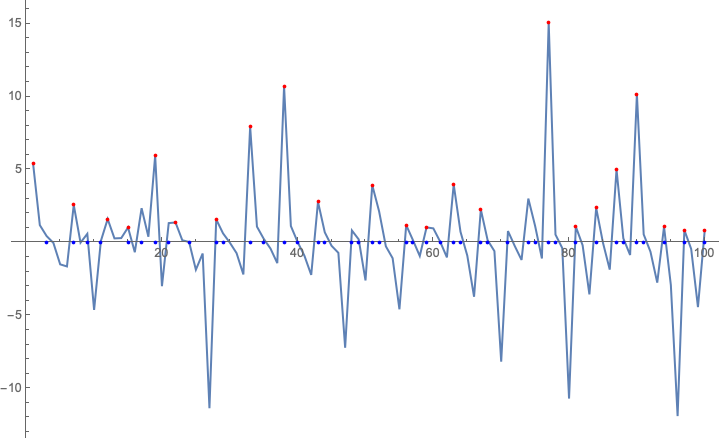
For a list of values, try FindPeaks and CrossingDetect. The latter may not satisfy your requirements.

proofN = proof // N;
peaks = FindPeaks[proofN];
zeros = CrossingDetect[proofN]*Range@Length@proofN // Thread[{#, 0}] & // DeleteCases[{0, 0}];

ListLinePlot[proofN,
 PlotRange -> All,
 Epilog -> {Red, Point@peaks, Blue, Point@zeros},
 ImageSize -> Large]

By "graphic" do you mean an image? If so, please attach an example to your post.

If you know the function corresponding to the graph then you can try solving f == 0 to get the roots (crossing abscissa) and solving for f' == 0 to get the local minima/maxima or point of inflection.