Hi, I have the following sum to compute numerically using wolfram mathematica and i cant seem to succeed limiting my variables as intended. The sum is:
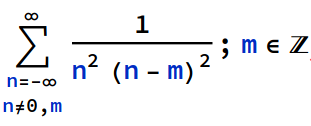
I tried using ConditionalExpression as follows:
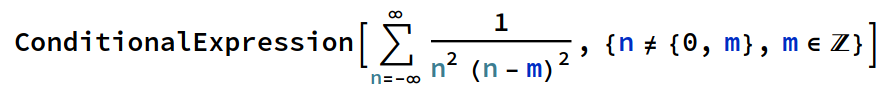
But to no avail. Code for copying:
ConditionalExpression[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = \(-\[Infinity]\)\), \(\
\[Infinity]\)]
\*FractionBox[\(1\), \(
\*SuperscriptBox[\(n\), \(2\)]
\*SuperscriptBox[\((n - m)\), \(2\)]\)]\), {n != {0, m},
m \[Element] Integers}]
Does anybody know how to write the conditions properly so mathematica will solve the summation?
edit: I have also tried the following way, but still the compiler doesn't recognize m,n from the conditions in the actual summation:
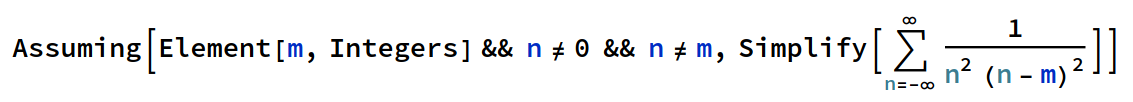
code for copy:
Assuming[Element[m, Integers] && n != 0 && n != m, Simplify[\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(n = \(-\[Infinity]\)\), \(\
\[Infinity]\)]
\*FractionBox[\(1\), \(
\*SuperscriptBox[\(n\), \(2\)]
\*SuperscriptBox[\((n - m)\), \(2\)]\)]\)]]
Thanks for helping! :>