Hi I'm trying to fit a Voigt distribution to a set of data, a Voigt distribution is a Gaussian Distribution + a Lorentzian Distribution(I have Mathematica 8).
So far i had found how to fit a Gaussian to my data, but when i tried to fit a Lorentzian, the program doesn't give nothing like my data
This is the code for the Gaussian
data = Import "C:/Users/Greg6r56/Desktop/s12Rammantest/normref.txt","Table"];
P1 = ListPlot[data, PlotRange -> {{450, 600}, {0, 1.2}}];
P3 = NonlinearModelFit[data, {Exp[-((x - s)^2/(2*m^2))] + n, {550 > s > 500, m > 0}}, {s,m, n}, x, MaxIterations -> 5000];
P4 = Normal[P3];
P5 = Plot[P4, {x, 450, 600}, PlotStyle -> Red, PlotRange -> All];
P3["BestFitParameters"]
Show[P1, P5]
and i obtain the following
{s -> 520.447, m -> 2.27856, n -> 0.0121122}
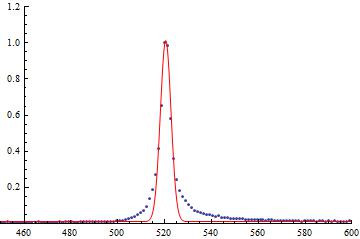
so far so good
but now for the Lorenztian
L = PDF[CauchyDistribution[a, b], x] + k;
L3 = NonlinearModelFit[data, {L, {550 > a > 500, b > 0}}, {a, b, k},x, MaxIterations -> 1000];
L4 = Normal[L3];
L5 = Plot[L4, {x, 450, 600}, PlotStyle -> Red, PlotRange -> All];
L3["BestFitParameters"]
Show[P1, L5]
and this is my outcome wich is notting like my data :s
{a -> 501.841, b -> 8.32944, k -> 0.0155552}
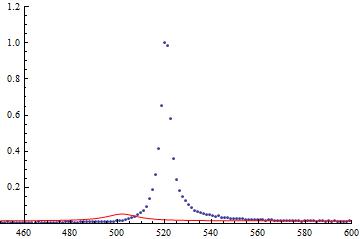
I hope someone could helpe me
Regards
P.S.
I attached the code and the data file
 Attachments:
Attachments: