I am stuck reading a passage from Jonathan Gorard's paper about relativity in the Wolfram model. At page 11, there is the definition of a "downward planar embedding".
Definition 11 A “downward planar embedding” is an embedding of a directed, acyclic graph in the Euclidean plane, in which edges are represented as monotonic downwards curves without crossings.
Then, he considers to embed a causal graph into the discrete “Minkowski lattice” $ \mathbb{Z}^{n,1}$ and to label the updating events according to their integer coordinates on the lattice.
There are many ways to embed a planar graph into the lattice, therefore I expect that these coordinates depend on the chosen embedding.
In the paper, follows the definition of the discrete Minkowski norm and the timelike/lightlike/spacelike separation of two events, and then, after a few sentences, the passage I cannot understand.
From our definition of the discrete Minkowski norm and the properties of layered graph embedding, we can see that a pair of updating events are causally related (i.e.connected by a directed edge in the causal graph) if and only if the corresponding vertices are timelike-separated in the embedding of the causal graph into the discrete Minkowski lattice $ \mathbb{Z}^{n,1}$, as required.
I don't understand how this statement could be true. Consider for example a simple causal graph constituted only of two events, where event 1 has a directed edge towards event 2 (i.e. event 1 is "the cause" of event 2). This graph is planar and so it is possible to perform a downward planar embedding in the Minkowski lattice $ \mathbb{Z}^{1,1}$ (just one spatial dimension to make things easier). Here I have drawn two possible embeddings of such graph.
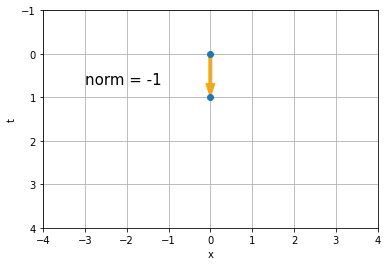
In the first case, the events are labelled by the coordinates (0,0) and (1,0) and therefore their spacetime separation is -1 and they are timelike separated.
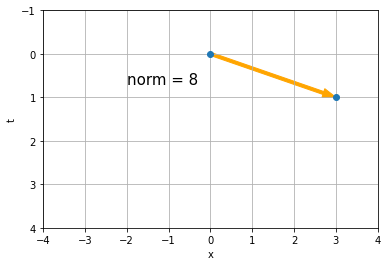
But in the second case, which is still a perfectly fair "downward planar embedding" by the definition given, the events have coordinates (0,0) and (1,3) and are therefore spacelike separated with norm 8.
The fact that the sign of the spacetime separation is dependent on the chosen embedding seems in contradiction with the statement quoted.
Can someone explain what am I missing here? Thank you