In this post, I would like to describe the properties that I think are required for a formal definition of a foliation of a causal graph. I will start with the definitions given in this recent paper (Algorithmic Causal Sets and the Wolfram Model by Jonathan Gorard) and show that some requirement must be relaxed in order to always guarantee the existence of a foliation. I will then propose a slightly different definition that in my opinion could be better suited for the wolfram model.
What is a foliation?
Given a causal graph, it defines a partial ordering on the set of events, denoted with the symbol $\prec$.
Definition 1 given two events x and y, we say that x "causally precedes" y (denoted $x \prec y$) iff either $x=y$ or there is a future directed path in the causal graph that starts on x and ends on y.
If we respect this partial ordering, we have still a lot of freedom to choose an order in which we perform the updates. Choosing the order of the updates means assigning a discrete time coordinate to each event, or equivalently, slicing the causal graph in a sequence of spacelike hypersurfaces.
The properties of a good foliation
In Gorard's article, there is a beautiful formal definition of a foliation. I like it because all the properties he requires from a foliation seem just to nail down the concept perfectly. From what I understand, Gorard defines a foliation as a sequence of hypersurfaces $\Sigma_i$, where each hypersurface is a subset of the set of the events $\mathcal{M}$. And the following is required:
- $ \forall j \neq j$ $\Sigma_i \cap \Sigma_j = \emptyset$: the hypersurfaces must be disjoint.
- $\bigcup \Sigma_i = \mathcal{M} $: we are foliating all the causal graph
- each $\Sigma_i$ must be "achronal" meaning that for every couple of events $x,y \in \Sigma_i$, they cannot be causally related. i.e. $x \prec y$ and $y \prec x$ must both be false.
- the Cauchy development of each hypersurface must be the whole $\mathcal{M}$. In other words, every event of $\mathcal{M}$ either causally precedes some event on $\Sigma_i$, or is causally preceded by some event on $\Sigma_i$, or is part of $\Sigma_i$ itself.
- Causal order must be preserved: there cannot exist two events $x \in \Sigma_i$ and $y \in \Sigma_j$ so that $i<j$, but at the same time $y \prec x$
This is a personal rephrasing which I think is equivalent to what stated in the article. Points 2 and 5 were added by me, because they were not stated explicitly in the article, but I think they can be inferred from the context.
A good foliation may not exist
As I have said, I like the definition given, because it relates immediately to the concept of Cauchy surface in a continuous manifold. Unfortunately, these requirements may be too stringent to guarantee the existence of such a foliation. Consider the following causal graph:
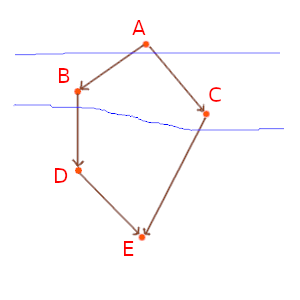
I will now try to build a foliation only to conclude that it is not possible.
Let's start from the first hypersurface. It must contain A because A causally precedes every other event, so using any other event to build the first hypersurface would violate point 5. So it must be A. A and what else? Nothing, because adding any other event would render the surface not achronal.
For the second hypersurface we can use B and C because if we remove either of them would violate point 4, since B and C are not in the Cauchy development of each other.
When trying to construct the third hypersurface we find some problems: If I only use D, then C is not in the Cauchy development of my $\Sigma_3$. If I only use E I am violating point 5, because D causally precedes E. If I use both E and D, then the surface is not achronal anymore.
Therefore, I am not able to foliate this causal graph according to the definition given.
Conclusion
If we want the foliation to be well defined, we must relax some of the requirements. I think a good compromise would be to drop the achronal requirement.
Even though the idea of an infinitely "thin" surface, like a Cauchy surface, is appealing, I think that in the context of Wolfram's model we could allow this surface to have some thickness. When defining a foliation we are actually defining a reference system or observer. We know that an observer with finite computational capabilities must perform some form of "coarse graining" an therefore could not be able to distinguish if a surface is perfectly thin or if some events inside the surface have a causal relation.
Please, tell me if this does make sense to you.